群(數學概念)

在數學中，群表示一個擁有滿足封閉性、結合律、有單位元、有逆元的二元運算的代數結構，包括阿貝爾群、同態和共軛類。

基本介紹

• 中文名：群
• 外文名：group
• 含義：數學概念
• 例子：置換群，一般線性群等
• 相關定義：阿貝爾群、同態、共軛類等
• 性質：封閉性、結合律、單位元和逆元

定義

若集合 ，在 上的二元運算（該運算稱為群的乘法，其結果稱為積） 構成的代數結構 ，滿足：

1. 封閉性：即G的任意兩個元素在 下的運算結果都是該集合的一個元素。（ ， ）。

2. 結合律： ， ；

3. 單位元： 中存在元素 ，使G中任一元素 與之相乘（包括左乘和右乘）的結果都等於 本身。（ ，使 ，有 ）；

4. 逆元： ， ，使得 ， 稱為 的逆元，記為 。（逆元具有唯一性，即：由 可以推出 ）

則 稱為一個群，或乘法群。

有時由於上下文的原因，群上的二元運算亦可稱為加法，此時該運算通常記為 ，群元素的運算也被記為如同 的形式，而群也可被稱為加法群。此種情況下，往往加法還有可交換的性質。

簡單例子

例1

在普通乘法下是群。

證：1)封閉性：1×1=1 (-1)×(-1)=1 (-1)×1=-1 1×(-1)=-1

2)結合律：成立

3)單位元：1

4)逆元素：1的逆元是1，-1的逆元是-1

例2

在mod n的加法下是群.

證：1)封閉性：除以n的餘數只能是 ，故封閉性成立

2)結合律：成立

3)單位元：0

4)逆元素：對任意元素a有 ，a的逆元

置換群

定義 為集合 上所有雙射的集合，並定義合成映射 ，這裡 是 的任意元素。 構成一個群，這個群被稱為置換群，記為 或 。

例集合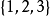 的三個元素置換群組成 .

一般線性群

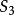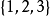
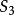
定義 為所有n階實可逆方陣的集合，乘法 為矩陣乘法，則 構成一個群。

這個群稱為一般線性群，記為 。

相關定義

阿貝爾群

若一個群 滿足交換律：對 的任意兩個元素 ，總有 a·b=b·a；

則稱群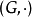 為阿貝爾群，也稱為加法群。

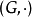
例如，群 就是一個阿貝爾群；群 和 亦然。

同態

若對於兩個群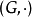 和 ，有映射 滿足以下條件：

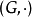
對G中任意元素a,b，都有 ；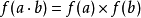

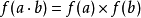
則稱映射 為群 到群 的同態。

如果映射 為單射，則稱 為單同態。

如果映射 為雙射，則稱 為同構。

易證得，同態有如下性質：

其中 是 的單位元， 是 的單位元。

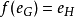
經典的同態有

是阿貝爾群 到阿貝爾群 的同態。

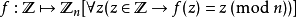
經典的同構有：

(1)

是正實數乘法群到實數加法群的同構。

(2)

其中 ， 是 的原根。

映射 是 到 的同構。

共軛類

一般可以把 中任意一個置換p分解為若干不相交的循環乘積。

P=( … )( … )….( … )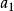

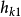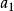
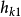
其中 ，設k階循環出現的次數為 ,用 表示，則 中置換的格式為 ... 。

例：(1)(23)(4 5 6 7)的格式是 。