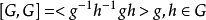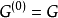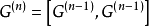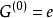相關詞條
- 換位子群
在抽象代數中,一個群的換位子群或導群,是指由這個群的所有交換子所生成的子群,記作[G,G]、G′或G(1) 。每個群都對應著一個確定的交換子群。在一個群G...
- 扭結群
若G的換位子群是 ,則 是無限循環群Z,扭結群是扭結型的不變數,但具有同構扭結群的扭結不一定等價,因此尋找儘可能精細的扭結不變數是扭結研究中的一個重要問題[2...
- 交換子
在抽象代數中,一個群的交換子或換位子是一個二元運運算元。設g及h 是群G中的元素,他們的交換子是g-1h-1gh,常記為[g, h]。只有當g和h符合交換律(即gh ...
- 格序單群
是單群在格序群範疇中的推廣。沒有真L理想的格序群稱為格序單群或L單群。若全序集T是2齊次的,則A(T)的換位子群B(T)是l單的。 [2] ...
- 特殊酉群
典型群是一類重要的群。一般線性群、酉群、辛群、正交群,以及它們的換位子群、對中心的商群等統稱為典型群。實數域和複數域上的典型群是李群的重要例子,它們的...
- 正則p群
有限p群P,若對P的任何二元二,y恆可找到由二,y生成的子群<二,y>的換位子群<二,y>‘中的若干個元‘,,‘:,…,‘:,使}xy)0=x0y0cP}..cc,則稱p為...
- 華羅庚文集
5群U1n(K,H)(n=2v)6 Un(K,H)的換位子群(n=2v)第九章 特徵數≠2的域上的正交群的構造(v≥1)1 複習2由2平延所演成的群...
- 劉合國
58. 冪零群的一個反例,中國科學,40:10(2010), 943-950.59. 換位子群為p階群的有限 群的自同構群,中國科學,40:11(2010), 1055-1078....
- 高階K群
(R) _二,<BGL <R ) )的換位子群.在同倫意義下,必有惟一的一個非循環映射f: BGL<R) --> BGL<R)-',使E(R)為二,<f)的核.環R的K群定義為空間...
- 同倫群
同倫群與同調群的一些基本關係:對於連通復形K的多面體|K|,1維同調群同構於基本群的交換化,即:這裡[π1(|K|),π1(|K|)]表示基本群π1(|K|)的換位子群...
- 段學復
從80年代初起,段學復和王萼芳的學生徐明曜、唐守文等人在上述幾篇論文的思想指引下和發展中進行工作,在p群的冪結構和換位子結構之間的聯繫上取得了研究成果。唐...
- 正契約倫序列
同倫群與同調群的一些基本關係:對於連通復形K的多面體|K|,1維同調群同構於基本群的交換化,即:這裡[π1(|K|),π1(|K|)]表示基本群π1(|K|)的換位子群...
- 結合代數
1933年中山正、松島與三證明了局部域上單代數的換位子群等於換 1元素群。王湘浩在1950年證明了上述二群在代數數域情形下仍相等,而且在一般域的情形下當指數無平方...
- 相對同倫
基本群是從單位閉區間I到拓撲空間X的閉路的同倫等價類和其運算得到的。相對同...這裡[π1(|K|),π1(|K|)]表示基本群π1(|K|)的換位子群。高維同倫群...
- 穩定同倫群
同倫群與同調群的一些基本關係:對於連通復形K的多面體|K|,1維同調群同構於基本群的交換化,即:這裡[π1(|K|),π1(|K|)]表示基本群π1(|K|)的換位子群...
- 同倫型不變性質
同倫群與同調群的一些基本關係:對於連通復形K的多面體|K|,1維同調群同構於基本群的交換化,即:這裡[π1(|K|),π1(|K|)]表示基本群π1(|K|)的換位子群...