群是一種只有一個運算的、比較簡單的代數結構;是可用來建立許多其他代數系統的一種基本結構。
同倫群(homotopy groups)基本群的高維推廣。基本群是從單位閉區間I到拓撲空間X的閉路的同倫等價類和其運算得到的。
基本群亦稱一維同倫群。對一個拓撲空間聯繫一個群的代數結構。
基本介紹
- 中文名:同倫群
- 外文名:homotopy groups
- 領域:群論
- 定義:基本群的高維推廣
- 對象:拓撲空間X的閉路的同倫等價類
- 重要人物:赫萊維茨
概念及性質
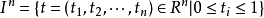
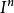

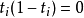
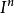

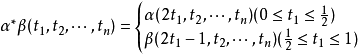

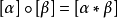

群
基本群
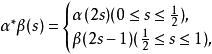
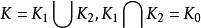
群是一種只有一個運算的、比較簡單的代數結構;是可用來建立許多其他代數系統的一種基本結構。
同倫群(homotopy groups)基本群的高維推廣。基本群是從單位閉區間I到拓撲空間X的閉路的同倫等價類和其運算得到的。
基本群亦稱一維同倫群。對一個拓撲空間聯繫一個群的代數結構。
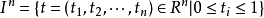
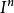

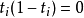
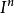

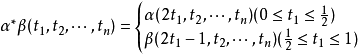

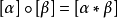

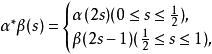
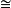
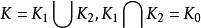
群是一種只有一個運算的、比較簡單的代數結構;是可用來建立許多其他代數系統的一種基本結構。同倫群(homotopy groups)基本群的高維推廣。基本群是從單位閉區間I到...
第二同倫群(second homotopy group)基於同倫的一類阿貝爾群.將群的呈示看做二維復形而得到的第二同倫群.是組合群論研究的重要對象.設P=(X;R)是群G的一個呈示...
同倫群(homotopy groups)是基本群的高維推廣。基本群是從單位閉區間I到拓撲空間X的閉路的同倫等價類和其運算得到的。相對同倫(relative homotopy)是同倫群的推廣。...
同倫概念的直觀解釋就是連續變形,以此為基礎定義的基本群被稱為同倫群。最早論及同倫群的是法國數學家龐加萊,他於1895年引進的復形基本群被稱為第一同倫群。1912...
群是一種只有一個運算的、比較簡單的代數結構;是可用來建立許多其他代數系統的一種基本結構。基本群亦稱一維同倫群。同倫群(homotopy groups)是基本群的高維推廣。...
同倫群提供了從拓撲到代數的另一種過渡,其幾何意義比同調群更明顯,但是極難計算。同倫群的計算,特別是球面的同倫群的計算問題刺激了拓撲學的發展,產生了豐富多彩的...
周學光,數學家。主攻代數拓撲學,主要成就涉及同倫論,特別是(n-1)連通的n+r維多面體的倫型以及球面同倫群等領域。...
P素分支(p-primary component)一類特殊同倫群的子群.同倫群二(S")中,階為素數p的方冪的元素構成的子群稱為二(S")的p素分支,並記為二(S"sp>.當p=2時,...
第五章 同倫群21.絕對同倫群和相對同倫群的定義例22.覆疊同倫.覆疊空間的同倫群和閉路空間23.球面同倫群的若干結果.裝配流形霍普夫不變數...
誘導同態是線性映射在張量代數上的開拓。誘導同態滿足的自然性,是同倫群的一個重要性質。...
博特定理是同倫群的周期性定理,是關於從球面到複數域上一般線性群的連續映射性質的一個定理。...
在數學領域代數拓撲學的同倫論中,懷特黑德定理說,拓撲空間X和Y之間的連續映射f,誘導出所有同倫群之間的同構,則當X和Y是連通,並都有CW復形的同倫型的時候,f是...
(4)證明了絕對同倫群間的乘法不只一種。張素誠服務生產 編輯 關於科學研究,張素誠主張既重視學術歷史發展中積累了的經驗,研究學術上重要的特殊矛盾,又重視實際工、...
全空間的同調關係問題,並由此證明了同倫論中最重要的一般結果:除了以前知道的兩種情形之外,球面的同倫群都是有限群;引進了局部化方法把求同倫群的問題加以分解,得出...
同倫概念的直觀解釋就是連續變形,以此為基礎定義的基本群被稱為同倫群。最早論及同倫群的是法國數學家龐加萊,他於1895年引進的復形基本群被稱為第一同倫群。1912...
拓撲不變數的定義是:兩個同構的拓撲空間之間相同的內秉性質。拓撲空間的同胚映射存在問題被轉移到拓撲不變數的構造。由此,產生了許多的拓撲不變數如同倫群、同調群。...
這條定理是漢斯·弗勒登塔爾在1937年證明,說明了把一個空間取懸垂時,這個空間的同倫群的表現。[1] 參考資料 1. 弗勒登塔爾懸垂定理 .7[引用日期2015-04-29] ...
奇P素分支,英文是odd p-primary component,是一類特殊同倫群的子群.。...... 奇P素分支,英文是odd p-primary component,是一類特殊同倫群的子群.。...
近年來發覺出五族球面穩定同倫群的不可分解新元素族中文百科內容由網友共同編輯,如您發現自己的詞條內容不準確或不完善,歡迎使用本人詞條編輯服務(免費)參與修正。立即...
托姆定理(Thom theorem)是關於托姆空間的同倫群同構於定向配邊群的定理。...... 托姆定理(Thom theorem)是關於托姆空間的同倫群同構於定向配邊群的定理。...
1 定義 2 基本群與二階同倫群 拉格朗日-格拉斯曼流形定義 編輯 拉格朗日-格拉斯曼流形(Lagrangian-Grassmannian)是實辛向量空間中拉格朗日子空間上的光滑流形。若向量...
稱為從k階同倫群到k階(整係數)同調群的胡列維茨同態。當k=1且X道路連通時,胡列維茨同態等價於標準的阿貝爾化映射胡列維茨定理聲明,若X是(n-1)-連通空間,...
表示托姆空間的穩定同倫群,即當n>i 時,這樣,當 一定時,與n無關,我們把它稱為托姆譜 的 維穩定同倫群。這樣求n的問題化為計算托姆譜的同倫群的問題。(...
