誘導同態是線性映射在張量代數上的開拓。誘導同態滿足的自然性,是同倫群的一個重要性質。
基本介紹
- 中文名:誘導同態
- 外文名:induced homomorphism
- 適用範圍:數理科學
定義介紹
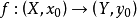

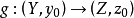

同倫群
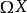
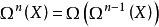
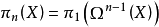
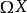
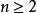


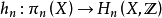
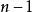
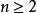
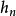
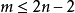
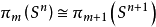
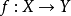
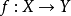

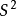
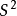

誘導同態是線性映射在張量代數上的開拓。誘導同態滿足的自然性,是同倫群的一個重要性質。
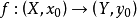

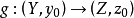

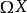
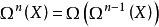
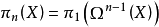
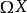
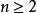


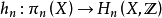
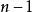
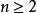
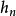
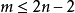
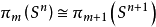
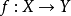
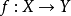

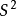
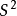
誘導同態是線性映射在張量代數上的開拓。誘導同態滿足的自然性,是同倫群的一個重要性質。...
他首次證明了本質,但是零調的映射的存在性,且基本性質不能用誘導同調同態來檢驗。1941年,他建立了H空間,並在研究H空間的同調以及上同調時,又建立了霍普夫代數。...
交叉同態(crossed homomorphism)亦稱導映射,一種特殊的映射。設M是左G模,f:G→M是一個映射。若對任意σ,τ∈G,都有f(στ)=σf(τ)+f(σ),則稱映射f...
雙同態(bihomomorphism)是一種特殊的同態。指雙模之間的同態。設G與G’是兩個群,如果有一個由G到G’的映射σ,使σ (ab)=σ(a)σ(b)對所有的a,b∈G都...
層同態(sheaf homomorphism)是兩類之間的映射誘導出的一個群同態。設(F,π,X)與(F′,π′,X)是X上的兩個群層,若連續映射A:F→F′滿足π′A=π,且對...
德拉姆同態是聯繫微分流形 M 上的德拉姆上同調群與奇異上同調群的一個自然同態。...... 與上邊緣運輸,d,δ 可交換,因此誘導上同調群之間的同態這個同態稱為德...
覆疊空間分類定理(classification theorem ofcovering spaces)關於覆疊空間等價的一條重要命題.設(X,p)是X的覆疊空間,則誘導同態 p,:},<X,b)~}r} <X ,a...
L收縮(L-retract)由L同態誘導出的概念.設M,N是f模,若存在L同態。:M}N和Y:N->M,使得。Y - 1.},,則稱N為M的一個L收縮,其中1N表示N的恆等L同態.f...
單純鏈映射(simplicial chain map)是由單純映射決定的鏈映射。鏈映射是聯繫復形的鏈群之間的一種系列同態。為了使復形的鏈群之間的同態能誘導出同調群之間的同態,...
