基本介紹
- 中文名:德拉姆同態
- 外文名:de Rham homomorphism
- 適用範圍:數理科學
簡介,概述,具體內容,德拉姆上同調群,
簡介
概述
具體內容
設 是它的對偶,即其中的每一個元素是M上一切可微奇異p單形到R的一個映射 f,這樣的f稱為M上的可微奇異p上鏈,令
是它的對偶,即其中的每一個元素是M上一切可微奇異p單形到R的一個映射 f,這樣的f稱為M上的可微奇異p上鏈,令

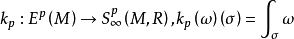





德拉姆上同調群
(de Rham cohomology group)
這是1930年由德拉姆(de Rham,G.-W.)給出的,他建立了微分流形的微分結構與拓撲結構的一個重要關係。

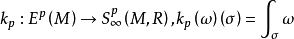





德拉姆同態是聯繫微分流形 M 上的德拉姆上同調群與奇異上同調群的一個自然同態。...... 德拉姆同態是聯繫微分流形 M 上的德拉姆上同調群與奇異上同調群的一個...
德拉姆定理是德拉姆同態為同構的定理。德拉姆定理還有另一個等價形式:設M為緊微分流形,則對每個整數p,p維德拉姆上同調群與p維可微奇異同調群的對偶同構。...
群是一種只有一個運算的、比較簡單的代數結構;是可用來建立許多其他代數系統的一種基本結構。商空間是一個線性空間模一個子空間所得的線性空間。德拉姆上同調群(...
德拉姆復形(de Rham complex)是一種與微分形式相關的鏈復形,亦稱為德拉姆鏈復形。...... 同態∂q稱為鏈復形的邊緣運算元,群Cq及其子群:Zq(C)=ker∂q,Bq...
數學上,陳-韋伊同態(英語:Chern–Weil homomorphism)是陳-韋伊理論的基本構造,將一個光滑流形M的曲率聯繫到M的德拉姆上同調群,也就是從幾何到拓撲。這個理論由...
