概念
具體說來,設
M是一個Hausdorff空間。
U是
M的
開集,
h是
U到
n維歐氏空間
R的開集(常取為單位球內部或立方體內部等等)上的一個
同胚映射,則(
U,
h)稱為一個坐標圖,
U稱為其中點的一個坐標鄰域。設
M為開集系{
Uα}所覆蓋,則(
Uα,
hα)的集合稱為
M的一個坐標圖冊。如果
M的坐標圖冊中任何兩個坐標圖都是
C相關的(坐標圖冊應該是極大的,即若任一坐標圖與坐標圖冊中每一個坐標圖都相容則其自身也屬於坐標圖冊),則稱
M有
C微分結構,又稱
M為
n維的
C微分流形。
C相關是指流形
M上同一點的不同坐標之間的變換關係是
C可微分的(
k=0,1,…,∞或
ω),依通常記號
C表示解析函式。具體來說, 如
p∈
Uα∩
Uβ,(
x,)(
x)(
i=1,…,
n)分別是
p在兩個坐標圖(
Uα,
hα),(
Uβ,
hβ)下的(局部)坐標,即那么它們之間的關係式可表為而
ƒ關於
x(
j=1,2,…,
n)具有直到
k次的連續導數。
k=0時,
M是拓撲流形;
k>0時,就是微分流形;
k=ω時,是解析流形。
C流形又常稱為光滑流形。如果微分流形
M是一個仿緊或緊緻拓撲空間,則稱
M為仿緊或緊緻微分流形。如果可選取坐標圖冊使微分流形
M中各個坐標鄰域之間的
坐標變換的
雅可比行列式都大於零,則稱這個流形是可定向的。球面是可定向的,麥比烏斯帶是不可定向的。
 1
1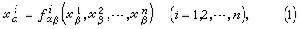 2
2同一拓撲流形可以具有本質上不同的微分結構。米爾諾(John Milnor)首先發現作為一個拓撲流形,七維球面上可有不同於標準微分結構的怪異微分結構。後來弗里德曼(Michael Freedman)等得出如下的重要結果:四維歐氏空間中也有多種微分結構,這與其他維數的歐氏空間只有惟一的微分結構有著重大區別。
類別
可微映射
設
φ是從
C流形
M到
C流形
N的連續映射,如果對於
N上的任意
Cr函式
ƒ,
M上的函式
ƒ。
φ總是
Cr的,則稱
φ是
Cr可微映射,或簡稱
Cr映射。如果
φ是從
M到
N上的
同胚,而且
φ和
φ都是
C的,則稱
φ為微分同胚,此時也稱
M與
N是微分同胚的微分流形。
映射的微分
設
φ是從
M到
N的
C映射。對
M上點
p的
切向量x可以如下地定義
N在點
φ(
p)處的切向量
x┡:這個對應
x→
x┡用d
φP表示,稱為
φ在點
p處的微分。微分d
φP是從
切空間TP(
M)到(
N)的
線性映射,有時也稱為
φ在切空間的誘導映射, 常用
φ*P或
φ*表示。利用對偶性,
φ也自然地誘導了從餘切空間到
T壩的線性映射,常記為(d
φP)或
φ壩或
φ。由
張量積運算,
φ還可以誘導對應點之間某些張量空間之間的線性映射。
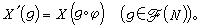 公式
公式 公式
公式 公式
公式子流形
設
M和
N是兩個
C流形,
φ:
M→
N是
C映射。如果微分d
φP在
M的每一點都是
單射,則稱
φ是浸入,而
φ(
M)稱為
N的浸入子流形。如果浸入
φ還是單射,則稱為嵌入,此時
φ(
M)稱為
N的嵌入子流形。
張量場
微分流形上可以定義
可微函式、
切向量、
切向量場、各種
張量場等對象並建立其上的分析學,並可以賦予更複雜的幾何結構以研究它們的性質。
光滑函式
流形M上的實數值
連續函式f:M →R是一個光滑函式,如果對每一個相容的坐標卡ρ:U→M, f(ρ):U→R是一個U上的光滑函式。因為坐標卡之間的坐標變換是光滑映射,這是一個良好的定義。特別的,光滑函式可以看成一種0階張量場。
向量場
設
p∈
M,
M在點
p處的一個切向量是指從F(
M)到
R的一個線性映射
x,使得對於任意的
ƒ,
g∈F(
M),滿足:對於在
p點的切向量
x1,
x2和實數
λ1,
λ2,定義
λ1
x1+
λ2
x2如下: 那么,點
p處的切向量全體構成一個
n維的實線性空間
TP,
TP稱為在
p處
M的切空間或切向量空間(也記為
TP(
M))。如果(
x,
x,…,
x)為點
p處的
局部坐標系,則由定義的
n個獨立的切向量,構成
TP的一組基,稱為自然
標架(或坐標標架)。
M的切向量全體構成以
M為底空間的
向量叢(見
纖維叢),稱為
M的切向量叢,簡稱
切叢。
M的切叢的一個截面稱為
M上的一個
向量場。在
局部坐標系中,向量場可表成的形式,式中ξ(
x)是坐標(
x)的
C函式。
TP的對偶空間稱為
M在點
p處的餘切空間,記為
T壩。
T壩中的元素稱為
餘切向量,也稱協變向量。
M的餘切向量全體構成
M的餘切
向量叢,簡稱
餘切叢,它的截面稱為
M上的一次
微分形式。 “1=2”
 條件
條件 公式
公式 1
1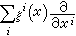 公式
公式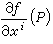 2
2一般張量場
由切空間和餘切空間通過張量積的運算可以得到
M在點
p處的各種(
r,s)型張量,
M的(
r,s)型的張量全體構成張量叢,它的截面就是
M上的一個(
r,s)型張量場(見多重線性代數、
張量)。
微分形式
在微分流形上還可以定義外微分形式(見
外微分形式)。
p次外微分形式(2)是一些微分的外積的線性組合,這些微分的外積是反對稱的,即是
p階反對稱協變張量,
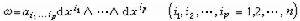 公式
公式 公式
公式M上p次外微分形式的全體構成一個實數域上的無限維向量空間
E。對外
微分形式可以進行加法運算(同次外微分形式可以相加),
外積運算(
p次外微分形式與
q次外微分形式的外積是一個(
p+
q)次外微分形式),還可以進行外微分運算及積分運算。在局部坐標下,外微分運算為
(3) 設ω∈
E且dω =0,則稱ω為閉形式。
M上
p次閉形式的全體構成
E的一個子空間記為Z。設ω∈
E,且ω=d
σ(
σ∈
E,則稱ω為正合形式。正合形式一定是閉形式。
M上
p次正合形式的全體也構成
E的一個子空間記為
B,
B嶅Z。商空間 (4)稱為
p次德·拉姆上同調群(de Rham cohomology group)。
 公式
公式結構
我們可以在微分流形上賦予不同的幾何結構(即一些特殊的張量場)。不同的幾何結構就是微分幾何不同的分支所研究的主要對象。
黎曼度量
仿緊微分流形均可賦予黎曼度量(見黎曼幾何),且不是惟一的。有了黎曼度量,微分流形就有了豐富的幾何內容,就可以測量長度,面積,體積等幾何量。
近復結構和複流形
微分流形M上的一個近復結構是M的切叢TM的一個自同構,滿足J·J=-1。如果近復結構是可積的,那么我們就可以找到M上的全純坐標卡,使得坐標變換是全純函式。這時我們得到了一個複流形。
辛流形
微分流形上的一個辛結構是一個非退化的閉的二次
微分形式。這樣的流形成為辛流形。
四維流形
在拓撲學中四維是一個非常特殊的維數。譬如
斯梅爾的
龐加萊猜想的證明只套用於大於四維的維數,他的h-配變定理不能套用於四維流形。而
弗里德曼的對四維龐加萊猜想的證明則更複雜。而且人們發現,存在四維拓撲流形,在其上不能賦予任何微分結構。而四維歐式空間是唯一一個存在怪異微分結構的歐式空間。
對四維微分流形的研究中具有里程碑意義的是英國數學家
西蒙·唐納森的工作。他的想法來源於理論物理中的
規範場理論。他由此定義了被稱為唐納森不變數的四維微分流形的不變數。後來物理學家賽博格和
愛德華·威騰將唐納森不變數簡化為一種更易於計算的不變數,後來被稱作賽博格-威騰不變數(Seiberg-Witten invariants)。這些不變數都大大推進了人們對四維微分流形的理解。
而對於四維拓撲流形,許多問題還沒有解決。其中最重要的是四維流形的光滑龐加萊猜測:(作為一個拓撲流形)四維球面上只存在標準的微分結構。
 1
1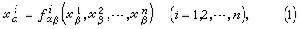 2
2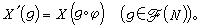 公式
公式 公式
公式 公式
公式 條件
條件 公式
公式 1
1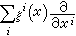 公式
公式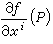 2
2 公式
公式
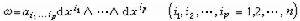 公式
公式 公式
公式