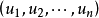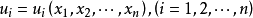基本介紹
- 中文名:雅可比行列式
- 外文名:Jacobian
- 別稱:雅可比式
- 提出者:雅可比
- 套用學科:高等數學
正文,證明,
正文
如果在一個連通區域內雅可比行列式處處不為零,它就處處為正或者處處為負。如果雅可比行列式恆等於零,則函式組是函式相關的,其中至少有一個函式是其餘函式的一個連續可微的函式。
證明
若因變數 對自變數
對自變數 連續可微,而自變數
連續可微,而自變數 對新變數
對新變數 連續可微,則因變數
連續可微,則因變數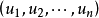 對新變數
對新變數 連續可微,且
連續可微,且




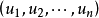


這可用行列式的乘法法則和偏導數的連鎖法則直接驗證。偏導數的連鎖法則也有類似的公式。如當(u,v)對(x,y,z)連續可微,而(x,y,z)對(r,s)連續可微時,便有

若上式中r能回到u,則

這時必須有 。
。

於是以此為係數行列式的聯立線性方程組中能把 解出來。
解出來。

由隱函式存在定理可知,在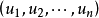 對連續可微的前提下,只須
對連續可微的前提下,只須 便足以保證
便足以保證 也對
也對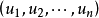 連續可微。這樣,連續可微函式組便在雅可比行列式不等於零的條件之下,在每一對相應點u與x的鄰近範圍內建立起點與點之間的一個一對一的對應關係。
連續可微。這樣,連續可微函式組便在雅可比行列式不等於零的條件之下,在每一對相應點u與x的鄰近範圍內建立起點與點之間的一個一對一的對應關係。
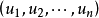


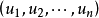
在n=2的情形,以Δx1,Δx2為鄰邊的矩形(ΔR)對應到(u1,u2)平面上的一個曲邊四邊形(ΔS),其面積ΔS關於Δx1,Δx2的線性主要部分,即面積微分是 。這常用於重積分的計算中。
。這常用於重積分的計算中。

如果在一個連通區域內雅可比行列式處處不為零,它就處處為正或者處處為負(其正負號標誌著u-坐標系的旋轉定向是否與x-坐標系的一致)。如果雅可比行列式恆等於零,則函式組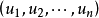 是函式相關的,其中至少有一個函式是其餘函式的一個連續可微的函式。
是函式相關的,其中至少有一個函式是其餘函式的一個連續可微的函式。