基本介紹
定義
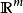






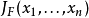
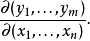


例子





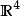


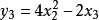


逆矩陣
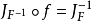






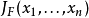
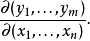









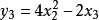


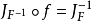
在向量微積分中,雅可比矩陣是一階偏導數以一定方式排列成的矩陣,其行列式稱為雅可比行列式。雅可比矩陣的重要性在於它體現了一個可微方程與給出點的最優線性逼近。...
雅可比行列式通常稱為雅可比式(Jacobian),它是以n個n元函式的偏導數為元素的行列式 。事實上,在函式都連續可微(即偏導數都連續)的前提之下,它就是函式組的微分...
卡爾·雅可比(Carl Gustav Jacob Jacobi,1804~1851),德國數學家。1804年12月10日生於普魯士的波茨坦;1851年2月18日卒於柏林。雅可比是數學史上最勤奮的學者之一,...
雅可比坐標系是一種特殊坐標系,指多體問題研究中常用的一種相對坐標系。一般取最大質量為第一體,討論第二體運動時取第一體為坐標原點;討論第三體運動時取第一、...
基本信息作者:方開泰/陳敏 出版社:高等教育出版社 出版年:2013-3 頁數:189 定價:22.10元 ISBN:9787040367881內容簡介《高等學校現代統計學系列教材:統計學中的矩陣...
J 表示f的雅可比矩陣,它的轉置為 。著名例子有 之間從極坐標 到直角坐標(x,y) 的坐標變換,在這例子裡有:這映射的雅可比矩陣為...
。它的雅可比矩陣是向量函式套用 編輯 向量函式的概念可直接推廣到任意維數的歐氏空間中去。像數學分析中討論實函式那樣,對向量函式也可以定義極限、連續、導數、微分...
本書文字大多為作者的原創,比如叉積的物理意義,克萊姆法則、雅可比矩陣、相似/契約矩陣、轉置矩陣/對偶、矩陣乘積的行列式等系列概念的幾何意義等,套用方面如使用...
概述克萊姆法則可以很有效地使用2×2矩陣來解決以下數式。 已知: 使用矩陣來表示時就是: x和y可以從克萊姆法則中得出: 以及 用3×3矩陣的情況亦差不多。 ...
在Rn(或定義了一組標準基的內積空間)里,函式的全微分和偏導數間的關係可以通過雅可比矩陣刻畫:設f是從Rn射到Rm的函式,f=(f1,f2,...fm),那么:...
密度為 r 的張量和普通張量一樣坐標變換,但是它還要乘以雅可比矩陣的行列式值的第 r 次冪。這個的最佳解釋可能是使用向量叢:其中,切叢的行列式叢是一個線叢,...
第2章 基於圖像雅可比矩陣的無標定手眼協調 2.1 圖像雅可比矩陣模型 2.2 圖像雅可比矩陣的例子 2.3 套用圖像雅可比矩陣建立視覺反饋控制 2.4 基於圖像雅可比矩陣的...
