基本介紹
- 中文名:偏導數
- 外文名:Partial derivative
- 別稱:導數
- 表達式:f'x(x0,y0)
- 提出者:Marquis de Condorcet
- 提出時間:1770
- 套用學科:數學
- 適用領域範圍:向量分析
- 適用領域範圍:微分幾何
- 意義:表示固定面上一點的切線斜率
在數學中,一個多變數的函式的偏導數,就是它關於其中一個變數的導數而保持其他變數恆定(相對於全導數,在其中所有變數都允許變化)。偏導數在向量分析和微分幾何中...
對於多元函式來說,若其一階偏導數仍是關於每個自變數的函式,並且一階偏導數對每個自變數的偏導數也存在,則說這個多元函式具有二階偏導數。以此類推,有三階偏導數...
導數(英語:Derivative)是微積分學中重要的基礎概念。一個函式在某一點的導數描述了這個函式在這一點附近的變化率。導數的本質是通過極限的概念對函式進行局部的線性...
偏導運算元是數學分析中偏導數概念的推廣。偏導運算元關於x的偏導運算元 設X,Y,Z是賦范線性空間,Ω是 X×Y 中的開集,f:Ω→Z,(x0,y0)∈Ω。若對於固定的y0...
已知二元函式z=f(u,v),其中u、v是關於x的一元函式,有u=u(x)、v=v(x),u、v作為中間變數構成自變數x的複合函式z,它最終是一個一元函式,它的導數就稱...
二階導數,是原函式導數的導數,將原函式進行二次求導。一般的,函式y=f(x)的導數y‘=f’(x)仍然是x的函式,則y’=f’(x)的導數叫做函式y=f(x)的二階...
一階導數的導數稱為二階導數,二階以上的導數可由歸納法逐階定義。二階和二階以上的導數統稱為高階導數。從概念上講,高階導數可由一階導數的運算規則逐階計算,...
對於雙曲函式sinh x,cosh x,tanh x等以及反雙曲函式arsinh x,arcosh x,artanh x等和其他較複雜的複合函式求導時通過查閱導數表和運用開頭的公式與 y=u±v...
在函式定義域的內點,對某一方向求導得到的導數。一般為二元函式和三元函式的方向導數,方向導數可分為沿直線方向和沿曲線方向的方向導數。...
導數(Derivative),也叫導函式值。又名微商,是微積分中的重要基礎概念。當函式y=f(x)的自變數x在一點x0上產生一個增量Δx時,函式輸出值的增量Δy與自變數...
近似導數是導數概念的一種推廣,其中普通極限用近似極限 (approximate limit)代替。最簡單的情形是,f(x)為實值函式,一般地,它是一個向量值函式,近似導數可以為...
一階偏微分方程是最簡單的一類偏微分方程。一階偏微分方程的幾何理論有悠久的歷史淵源,以後經過É.(-J.)嘉當等人的發展,在幾何學、力學和物理學中都有重大的...
包含未知函式的偏導數(或偏微分)的方程。方程中所出現未知函式偏導數的最高階數,稱為該方程的階。在數學、物理及工程技術中套用最廣泛的,是二階偏微分方程,習慣...
鏈式法則是微積分中的求導法則,用於求一個複合函式的導數,是在微積分的求導運算中一種常用的方法。複合函式的導數將是構成複合這有限個函式在相應點的 導數的乘積...
鏈式法則(英文chain rule)是微積分中的求導法則,用以求一個複合函式的導數。所謂的複合函式,是指以一個函式作為另一個函式的自變數。如設f(x)=3x,g(x)=3x+...
求導是數學計算中的一個計算方法,它的定義就是,當自變數的增量趨於零時,因變數的增量與自變數的增量之商的極限。在一個函式存在導數時,稱這個函式可導或者可微分...
滿足隱函式存在惟一性定理中的條件(i)-(iv),又設在D上還存在連續的偏導數 ,則由方程(1)所確定的隱函式 在其定義域 上有連續導函式,且隱...
對數求導法是一種求函式導數的方法。取對數的運算可將冪函式、指數函式及冪指函式運算降格成為乘法運算,可將乘法運算或除法運算降格為加法或減法運算,使求導運算計算...
定理2(充分條件): 設函式z = f(x,y)在點(x0,y0)的某領域內連續且有一階及二階連續偏導數,又fx(x0,y0) = 0,fy(x0,y0) = 0,令fxx(x0,y0) ...
形如y'+P(x)y=Q(x)的微分方程稱為一階線性微分方程,Q(x)稱為自由項。一階,指的是方程中關於Y的導數是一階導數。線性,指的是方程簡化後的每一項關於y...
舉個例子,若欲求z = f(x,y)的導數,那么可以將原隱函式通過移項化為f(x,y,z) = 0的形式,然後通過(式中F'y,F'x分別表示y和x對z的偏導數)來求解。...
費馬(Fermat)在一封給羅貝瓦(Roberval)的信中,提及計算函式的極大值和極小值的步驟,而這實際上已相當於現代微分學中所用,設函式導數為零,然後求出函式極點的...
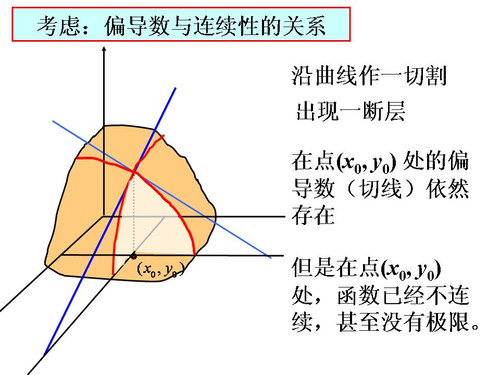
如果函式z=f(x,y)在點p0(x0,y0)處可微,則z=f(x,y)在p0(x0,y0)處連續,且各個偏導數存在,並且有f′x(x0,y0)=A,f′y(x0,y0)=B。...
此外,UNIPASS軟體提供了6種可靠性分析方法(FORM,SORM,MCS,ISM,RSM和MVBM)和三類可靠性靈敏度(在設計點處功能函式對隨機變數的偏導數,失效機率或可靠度指標對隨機...
