一元函式是指函式方程式中只包含一個自變數。例如y=F(x)。與一元函式對應的為多元函式,顧名思義函式方程中包含多個自變數。在工科數學基礎分析中:設A,B是兩個非空的實數集,則稱映射f:A→B為定義在A上的一元函式,簡稱函式。
基本介紹
- 中文名:一元函式
- 外文名:Function of One Variable
- 學科:數學
- 內容:函式方程式中只包含一個自變數
- 例子:y=F(x)
簡介
函式
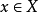












一元函式是指函式方程式中只包含一個自變數。例如y=F(x)。與一元函式對應的為多元函式,顧名思義函式方程中包含多個自變數。在工科數學基礎分析中:設A,B是兩個非空的實數集,則稱映射f:A→B為定義在A上的一元函式,簡稱函式。
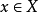











一元函式是指函式方程式中只包含一個自變數。例如y=F(x)。與一元函式對應的為多元函式,顧名思義函式方程中包含多個自變數。在工科數學基礎分析中:設A,B是兩個...
形如y=kx+b(k≠0)的函式稱為一元一次函式(linear function of one variable),一元一次函式y=kx+b(k≠0)具有下列性質:在平面直角坐標系中它的圖象是一條...
《一元函式微積分》結構清晰,概念準確,循序漸進,可讀性強,便於教學,且能夠啟發和培養學生的自學能力。全書共6章,內容包括函式、極限與連續、導數與微分、導數的...
設S 是集合,函式 f :S→S 稱為 S 上的一個一元運算。一元運算示例 編輯 (1) 求數的相反數是整數集合 Z 、有理數集合 Q 和實數集合 R 上的一元運算...
《高等數學1:一元函式微積分學》側重問題的發現與分析,注重數學思想的挖掘,幫助讀者學會如何進行數學猜測,如何從特殊現象中發現一般規律,不僅介紹數學知識,更注重概念...
《大學數學基礎教程(1):一元函式微積分》是普通高等教育“十五”國家級規劃教材《大學數學基礎教程》的第一分冊。介紹一元函式微積分與微分方程的基本知識,內容包括...
回歸分析只涉及到兩個變數的,稱一元回歸分析。一元回歸的主要任務是從兩個相關變數中的一個變數去估計另一個變數,被估計的變數,稱因變數,可設為Y;估計出的...
一元函式微積分典型題型及解題技巧內容簡介 編輯 本書根據《高職高專教育高等數學課程教學基本要求》一元函式微積分部分編寫,全書共九章,包括函式定義及其性質的套用...
《一元函式微積分與線性運算元》是 2015年5月科學出版社出版的圖書,作者是王栓宏。...... 《一元函式微積分與線性運算元》是 2015年5月科學出版社出版的圖書,作者是...
《高等微積分教程(上):一元函式微積分與常微分方程》是2014年清華大學出版社出版的圖書,作者是劉智新、閆浩、章紀民。...
《大學數學基礎教程1(一元函式微積分)》是普通高等教育“十五”國家級規劃教材《大學數學基礎教程》的第一分冊。介紹一元函式微積分與微分方程的基本知識,內容包括:...
標準型的一元三次方程aX^3+bX^2+cX+d=0(a,b,c,d∈R,且a≠0),其解法有:1、義大利學者卡爾丹於1545年發表的卡爾丹公式法;2、中國學者范盛金於1989年發表...
本冊包括集合及其運算,映射與函式,數列的極限,導數與微分,不定積分,微分中值定理,微分學在函式研究中的套用等內容。書名 大學數學教程(第1卷第1冊)一元函式微...
《高等數學基礎一元函式微積分與無窮級數》是2004年6月高等教育出版社出版的事情。...... 《高等數學基礎一元函式微積分與無窮級數》是2004年6月高等教育出版社出版...
《經濟數學基礎:一元函式微積分及其套用·機率論與數理統計》是2009年3月1日化學工業出版社出版的圖書。...
