基本介紹
- 中文名:偏導運算元
- 外文名:partial derivative
- 適用範圍:數理科學
簡介
關於x的偏導運算元
關於y的偏導運算元
性質
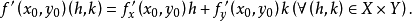
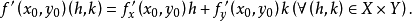
若對於固定的y0,以x為變元的映射g(x)=f(x,y0)在x0 F可微(相應地,G可微),則定義f在(x0,y0)關於 x 的偏 F 導運算元(相應地,偏 G 導運算元)為f'x...
)的結果。因此如果 是二階可微的實函式,則 的拉普拉斯運算元定義為:的拉普拉斯運算元也是笛卡兒坐標系 中的所有非混合二階偏導數:作為一個二階微分運算元,對於k≥ 2,...
Canny運算元先利用高斯平滑濾波器來平滑圖像以除去噪聲,Canny分割算法採用一階偏導的有限差分來計算梯度幅值和方向,在處理過程中,Canny運算元還將經過一個非極大值抑制...
圖像以除去噪聲,Canny分割算法採用一階偏導的有限差分來計算梯度幅值和方向,在處理過程中,Canny運算元還將經過一個非極大值抑制的過程,最後Canny運算元還採用兩個閾值...
圖像以除去噪聲,Canny分割算法採用一階偏導的有限差分來計算梯度幅值和方向,在處理過程中,Canny運算元還將經過一個非極大值抑制的過程,最後Canny運算元還採用兩個閾值...
圖像以除去噪聲,Canny分割算法採用一階偏導的有限差分來計算梯度幅值和方向,在處理過程中,Canny運算元還將經過一個非極大值抑制的過程,最後Canny運算元還採用兩個閾值...
全純函式滿足Cauchy-Riemann方組,該方程組含有兩個偏微分方程,也可以用復偏導運算元寫成一個。在非 導數的點的附近,全純函式是共形的 (或保角的,實際上就是...
§10.2 運算元定義和高階偏導統一形式 §10.3 統一偏導運算元的性質和運算規則 §10.4 高階齊次分解定理 第十一章 機械系統新的Hamilton框架及基於能量控制設計 §...
階弱偏導數,記做可以證明如果一個函式的 階弱偏導數存在,那么偏導數在幾乎處處...上幾乎處處定義的函式的線性運算元 滿足 且對於任何正整數 有 。索...
的坐標函式,那么定義其符號(symbol)是以(p1, ..., pk, q1, ..., qk)為自變數的函式,具體定義是去掉D的低階項,並將最高階項中的對pi求偏導的運算元換成...
