索伯列夫空間是數學裡由函式組成的賦范向量空間,主要用來研究偏微分方程理論,它以前蘇聯數學家С.Л.索伯列夫命名。
基本介紹
- 中文名:索伯列夫空間
- 外文名:Sobolev space
- 別名:索布列夫空間
索伯列夫空間的動機
弱導數
弱導數的動機
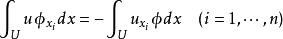
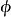
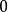
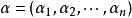
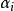
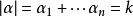
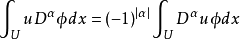
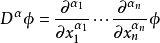
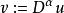


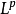
弱導數的定義
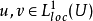
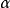
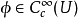
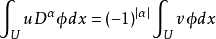


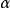
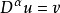
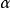
索伯列夫空間的定義
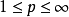
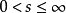
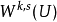
整數k的索伯列夫空間


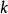
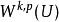
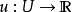

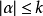
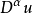
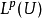
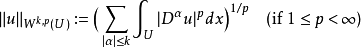

非整數s的索伯列夫空間
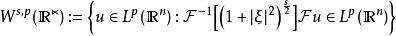
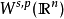

索伯列夫延拓運算元
延拓定理
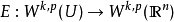
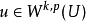
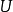
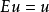
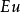
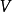
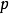
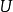
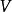
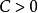
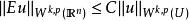
全延拓運算元
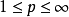
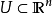
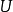
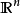
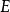
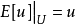
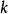

索伯列夫嵌入
Morrey不等式
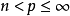
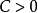
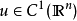
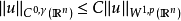
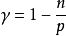
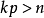
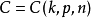
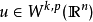
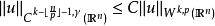
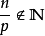
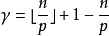
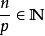
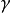
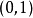
Gagliardo-Nirenberg-Sobolev不等式
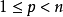

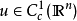
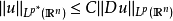

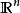
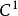
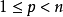
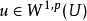
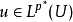
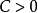
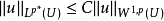

索伯列夫空間是數學裡由函式組成的賦范向量空間,主要用來研究偏微分方程理論,它以前蘇聯數學家С.Л.索伯列夫命名。
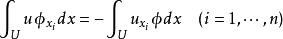
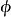
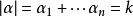
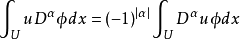
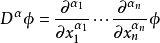
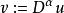


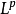
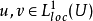
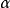
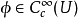
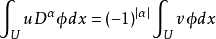


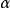
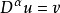
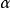
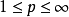
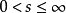
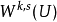


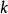
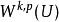
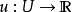

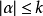
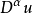
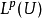
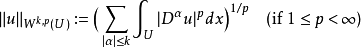

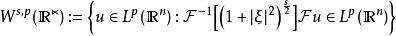
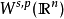

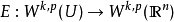
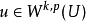
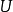
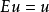
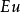
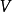
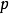
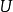
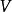
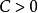
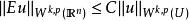
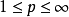
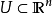
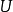
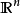
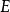
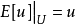
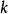

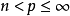
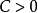
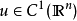
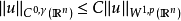
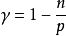
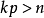
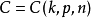
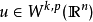
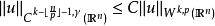
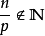
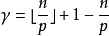
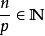
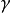
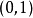
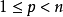

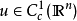
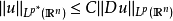

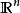
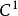
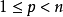
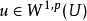
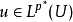
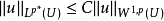
索伯列夫空間是數學裡由函式組成的賦范向量空間,主要用來研究偏微分方程理論,它以前蘇聯數學家С.Л.索伯列夫命名。...
泛函分析、索伯列夫空間和偏微分方程內容簡介 編輯 該書提出了一個連貫的、確切的、統一的方法將兩個來自不同領域的元素——泛函分析和偏微分方程,結合在一起,...
數學上,一個索伯列夫空間是一個由函式組成的賦范向量空間,對於某個給定的p≥ 1,它對一個函式f和它的直到某個k階導數加上有限Lp範數的這個條件。它以前蘇聯...
《索伯列夫空間講義》是2003年東南大學出版社出版的圖書,作者是王元明,徐君祥。...... 《索伯列夫空間講義》是2003年東南大學出版社出版的圖書,作者是王元明,徐君祥...
《索伯列夫空間和插值空間導論(英文)》是以作者研究生教程的講義為藍本整理擴充而成,全面講述了索伯列夫空間和插值理論。書中包括42章,每章儘可能多的包括研究生...
索伯列夫嵌入定理(Sobolev imbedding theorems)是索伯列夫空間最重要的性質,可以用索伯列夫不等式證明該定理。...
索伯列夫不等式(Sobolev inequalities)索伯 列夫空間最重要的性質.設X,Y是兩個巴拿赫空 間,它們滿足條件: 1.如果uEX,則uEY; 2.存在常數C}0,使得對任意uEX有...
貝塞爾位勢空間(Bessel potential spaces)是索伯列夫空間的一種推廣。...... 貝塞爾位勢空間(Bessel potential spaces)是索伯列夫空間的一種推廣。中文名 貝塞爾位勢...
舍蓋·劉維奇·索伯列夫(俄語:Серге́й Льво́вичСо́болев;1908年10月6日–1989年1月3日)是一位蘇聯數學家,主要研究領域是...
有時兩線性拓撲空間A,B間包含關係A<B同時還表示映射A→B是連續的,這時A<B表A單射入B。在函式空間,廣義函式的空間,索伯列夫空間方面有許多這類關係,最常見的...
尼倫伯格不等式(Nirenberg inequality)一種形式的索伯列夫空間內插不等式.設,f2CR”是一個具有限錐性質的n維有界區域,記 除非1<p<+}且L- j-n/p是非負整數...
對於這個情況的一個正確處理,我們可以採用索伯列夫空間(Sobolev space)的概念。[2] 參考資料 1. 熊金志, 胡金蓮, 袁華強,等. 支持向量回歸機的光滑函式研究[J]...
精確的定義和分解的證明需要用索伯列夫空間來表述問題。主要的思想就是索伯列夫空間提供了平方可積性和微分形式的柯西列收斂到極限形式的自然設定。這個語言使得我們...
基於泛函分析理論(巴拿赫空間,索伯列夫空間,再複製希爾伯特空間理論,運算元譜論,框架理論)、半參數模型理論、經驗過程理論、隨機過程統一中心極限理論、巴拿赫空間機率理論...
在數論、索伯列夫空間和非線性偏微分議程方面發表論文25篇,出版了專著《微分議程中的變分方法》。他單獨完成的科研成果《各嚮導性索伯列夫空間的嵌入定理》獲1986...
4.1.1廣義函式空間 4.1.2廣義函式的卷積與傅立葉變換理論 4.1.3線性偏微分方程的基本解 4.2索伯列夫空間論 4.2.1索伯列夫空間 4.2.2嵌入定理 4.3二階線性橢圓...
先驗估計是近代研究偏微分方程的一種基本方法和技巧。對偏微分方程定解問題,在解存在的假設下,通過方程係數、自由項及定解條件估計解在某個巴拿赫空間(一般是索伯...
高等數學、計算方法、微分方程的數值解、數學物理方程、線性代數與計算方法(全英語)、索伯列夫空間和偏微分方程的L^2理論以及有限元方法(雙語)等課程,發表教學論文...
這個定義可以延伸至M不是緊緻的情況:φ稱為調和映射,若φ限制到任一個緊緻區域上都是調和映射,換一個更通常的說法,就是若在索伯列夫空間H(M,N)中φ是能量...
講授過如下課程:《反應擴散方程》,《二階拋物型方程》,《廣義函式》,《索伯列夫空間》,《泛函分析》,《現代分析基礎》,《空間解析幾何》,《數學物理方法與積分...
對偏微分方程定解問題,在解存在的假設下,通過方程係數、自由項及定解條件估計解在某個巴拿赫空間(一般是索伯列夫空間或連續可微函式空間)中的範數的上界的不等式...
承擔研究生課程: 索伯列夫空間、橢圓問題有限元方法。[1] 參考資料 1. 尹哲 .山東師範大學[引用日期2015-09-14] 詞條標籤: 娛樂人物 , 人物 ...
《邊值問題的Galerkin有限元法》以索伯列夫空間為框架,介紹抽象的變分形式和Ritz-Galerkin法,基於peano餘項估計介紹索伯列夫空間插值理論,從而建立標準有限元法的...
擬微分運算元有界性(boundedness of pseu-dodifferential operators)擬微分運算元在某些函式空間上所滿足的範數關係.在諸如索伯列夫空間、赫爾德空間及別索夫空間等重要的...
碩士生課程:偏微分方程數值解、有限差分法、索伯列夫空間、譜方法引論博士生課程:體力學中的譜方法、函式空間與逼近、有限元分析馬和平學術成就 編輯 ...
