基本介紹
簡介



技術性討論


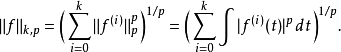

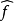
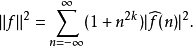
非整數k情況
p等於2
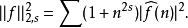

分數階微分


復插值
多維情況


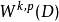



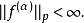

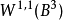



索博列夫嵌入


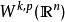

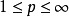

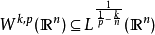
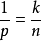

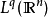







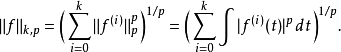

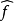
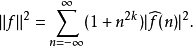
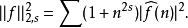





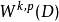



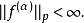

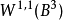





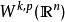

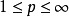

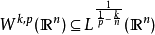
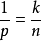

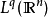

Sobolev空間技術性討論 編輯 我們從最簡單情況下的索博列夫空間開始,也就是單位圓上的一維情況。在這個情況下,索博列夫空間 定義為L的子集,使得f和它的直到k階...
索伯列夫空間是數學裡由函式組成的賦范向量空間,主要用來研究偏微分方程理論,它以前蘇聯數學家С.Л.索伯列夫命名。中文名 索伯列夫空間 外文名 Sobolev space ...
《廣義函式和Sobolev空間》是2008年西安交通大學出版社出版的圖書,作者是李開泰、馬逸塵。...
《Sobolev空間與偏微分方程引論》是2009年科學出版社出版的一本圖書,作者是王術。本書主要講述了偏微分方程一般理論的主要結果和研究方法。...
《Sobolev空間與變分原理》是2013年中國科學技術大學出版社出版的圖書,作者是張維弢。...
比如說當S是n維歐幾里德空間,而μ是S上的正則博雷爾測度的時候,可以證明,所有緊支撐的光滑函式的集合在( 中稠密。參考資料 1. Adams, Robert A. Sobolev ...
本書主要內容包括:預備知識、LP空間、Lorentz空間與Orlicz空間、Sobolev空間Ⅱ、有界變差函式等。...
奧爾利奇空間(Orlicz space)是Lp(1<p<∞)空間的推廣。 奧爾利奇是波蘭數學...廣義Orlicz-Sobolev空間W~(k,p(x))(Ω)[J]. 甘肅教育學院學報(自然科學版...
《希爾伯特空間及其套用導論》是2012年世界圖書出版公司出版的圖書,作者是德布納斯。 本書在原來版本的基礎上做了不少改動,新增加了一部分講述Sobolev空間,展開講述了...
《索伯列夫空間講義》是2003年東南大學出版社出版的圖書,作者是王元明,徐君祥。...... 4 實指數的Sobolev空間4.1 實指數Sobolev空間及其性質4.2 對偶空間H-s...
索伯列夫空間和有關的嵌入定理已成為研討偏微分方程理論必不可少的工具。本書...第十七章 加權Sobolev第十八章 各向異性Sobolev空間W1(pi)(G)中的嵌入定理...
在數學中,Lp空間是由p次可積函式組成的空間;對應的ℓp空間是由p次可和序列...Sobolev Spaces. New York: Academic Press. 1975. ISBN 978-0-12-044150-1...
閱讀《西安交通大學研究生教育系列教材:數學物理方程Hilbert空間方法》需要具備廣義函式和Sobolev空間理論、泛函分析、初等的偏微分方程理論和方法以及數理方程等基礎知識...
泛函分析、索伯列夫空間和偏微分方程 [1] 作者 Haim Brezis [1] 原版名稱 Functional Analysis, Sobolev Spaces and Partial Differential Equations [1] ISBN...
《索伯列夫空間和插值空間導論(英文)》是以作者研究生教程的講義為藍本整理擴充...32 sobolev‘s embedding theorem for besov spaces 33 the lions-magenes space...
索伯列夫嵌入定理(Sobolev imbedding theorems)是索伯列夫空間最重要的性質,可以用索伯列夫不等式證明該定理。...
索伯列夫不等式(Sobolev inequalities)索伯 列夫空間最重要的性質.設X,Y是兩個巴拿赫空 間,它們滿足條件: 1.如果uEX,則uEY; 2.存在常數C}0,使得對任意uEX有...
在數學分析中有一類關於Sobolev空間中的範數的索博列夫不等式。 這些不等式可以用於證明Sobolev嵌入定理,給出某些Sobolev空間的包含關係。而Rellich-Kondrachov定理指出...
在數學方面,龐加萊不等式是以法國數學家亨利·龐加萊(Henri Poincaré)命名的Sobolev空間理論的不等式。 不等式允許使用其導數上的邊界及其定義域的幾何來獲取函式...
