索博列夫不等式

在數學分析中有一類關於Sobolev空間中的範數的索博列夫不等式。 這些不等式可以用於證明Sobolev嵌入定理，給出某些Sobolev空間的包含關係。而Rellich-Kondrachov定理指出在稍強的條件下，一些Sobolev空間可以被緊嵌入到另一個空間。 這類不等式得名於謝爾蓋·利沃維奇·索博列夫。

基本介紹

• 中文名：索博列夫不等式
• 外文名：Sobolev inequality
• 學科：數學

一般Sobolev不等式

令U為R上帶有C邊界的有界開集。（U也可以無界，但這種情況下，它的邊界如果存在，則必須是充分好的。）假設u∈W(U)，考慮兩種情況：

1）k<n/p

這時u∈L(U)，其中

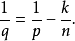
有估計

常數C只依賴於k,p,n和U。

2）k>n/p

這裡u屬於Hölder空間，更精確的：

其中

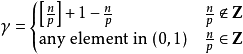
有估計

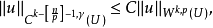
常數C只依賴於k,p,n,γ和U。

特殊情形

如果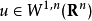，則u是有界平均振動函式且有

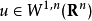
對於某個常數C只依賴於n。這個估計是龐加萊不等式的推論。