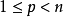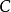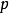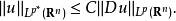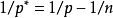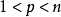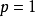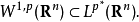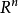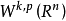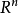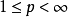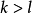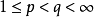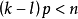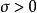基本介紹
- 中文名:索伯列夫嵌入定理
- 外文名:Sobolev imbedding theorems)
- 別稱:Sobolev嵌入定理
- 提出者:謝爾蓋·利沃維奇·索博列夫
- 提出時間:1938年
- 套用學科:數理科學
- 適用領域範圍:數學分析
定理內容,推廣,索伯列夫不等式,
定理內容
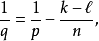

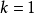
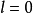
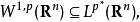

索伯列夫嵌入定理的第二部分用於嵌入到Hölder空間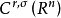 。如果
。如果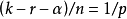 其中
其中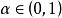 ,則有嵌入
,則有嵌入
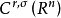
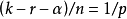
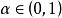
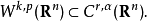
索伯列夫嵌入的這個部分可由Morrey不等式直接得出。直觀的說,這種包含關係表示足夠高階的弱導數存在性意味著一些經典導數的連續性。
推廣
索伯列夫嵌入定理對於有其他適當定義域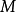 的索伯列夫空間
的索伯列夫空間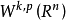 也成立。特別的,索伯列夫嵌入的兩個部分在滿足下列條件時成立:
也成立。特別的,索伯列夫嵌入的兩個部分在滿足下列條件時成立:
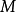
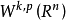
1)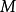 是
是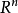 上有Lipschitz邊界的有界開集(或者邊界滿足錐條件);
上有Lipschitz邊界的有界開集(或者邊界滿足錐條件);
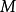
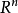
2)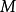 是緊黎曼流形;
是緊黎曼流形;
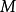
3)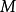 是有Lipschitz邊界的緊帶邊黎曼流形;
是有Lipschitz邊界的緊帶邊黎曼流形;
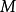
索伯列夫不等式
索伯列夫不等式,即Gagliardo–Nirenberg–Sobolev不等式,可以用於證明索伯列夫嵌入定理。
假設u是R上擁有緊支集的連續可微實值函式。對於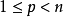 存在常數
存在常數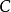 只依賴於
只依賴於 和
和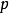 使得
使得