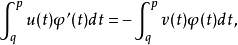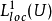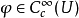弱導數

在數學中，弱導數（Weak Derivative）是一個函式的微分（強微分）概念的推廣，它可以作用於那些勒貝格可積（Lebesgue Integrable）的函式，而不必預設函式的可導性（事實上大部分可以弱微分的函式並不可微）。

基本介紹

• 中文名：弱導數
• 外文名：weak derivative
• 領域：數學
• 別稱：弱微分

定義

弱導數作用於那些勒貝格可積的函式，而不必預設函式的可微性。一個典型的勒貝格可積函式的空間是。在分布中，可以定義一個更一般的微分概念。

令 是一個在 中的勒貝格可積的函式，稱 是 的一個弱導數，如果

其中 是任意一個連續可微的函式，並且滿足 。

推廣到 維的情形，如果 和 是 中的函式（在某個開集 中局部可積），並且 是一個多重指標，那么 稱為 的 次弱微分，如果

其中 是一個任意給定的函式，即給定的支撐集含於 的無窮可微的函式。

如果 的弱導數存在，一般被記為 。可以證明，一個函式的弱微分在測度意義是唯一的，即如果有兩個不同的弱導數，其僅可能在一個零測集上存在差異。

例子

函式 在 並不可微，但具有以下被稱為符號函式的弱導數：

性質

如果兩個函式是相同函式的弱導數，那么它們除了在一個勒貝格測度為零的集合上以外相等，也就是說，它們幾乎處處相等。如果我們考慮函式的等價類，其中兩個函式是等價的如果它們幾乎處處相等，那么弱導數是唯一的。

此外，如果是可微的，那么它的弱導數與導數相同。因此弱導數是導數的推廣。更進一步，兩個函式的和與積的導數公式對弱導數也是成立的。