弱微分

在數學中，弱微分是一個函式的微分（強微分）概念的推廣，它可以作用於那些勒貝格可積（Lebesgue Integrable）的函式，而不必預設函式的可微性（事實上大部分可以弱微分的函式並不可微）。

一個典型的勒貝格可積函式的空間是L¹([a,b])。在分布中，可以定義一個更一般的微分概念。

基本介紹

• 中文名：弱微分
• 外文名：Weak Derivative
• 適用範圍：數理科學

定義

在數學中，弱微分是一個函式的微分（強微分）概念的推廣，它可以作用於那些勒貝格可積（Lebesgue Integrable）的函式，而不必預設函式的可微性（事實上大部分可以弱微分的函式並不可微）。

命u是一個在 中的勒貝格可積的函式，稱v 是u的一個弱微分，如果

，其中 是任意一個連續可微的函式，並且滿足 。

推廣到n維的情形，如果u和v是 中的函式（在某個開集U中局部可極，U是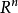 的子集），並且 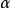是一個多重指標，那么v稱為u的 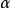次弱微分，如果 ，其中 是一個任意給定的函式，即給定的支撐集含於U的無窮可微的函式。

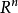
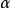
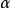
如果u的弱微分存在，一般被記為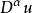 。可以證明，一個函式的弱微分在測度意義是唯一的，即如果有兩個不同的弱微分，其僅可能在一個零測集上存在差異。

實例

函式u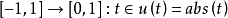： 在t=0並不可微，但具有以下被稱為符號函式的弱微分： ，t>0時v(t)=1，t=0時v(t)=0，t<0時v(t)=-1。

性質

如果兩個函式是相同函式的弱導數，那么它們除了在一個勒貝格測度為零的集合上以外相等，也就是說，它們幾乎處處相等。如果我們考慮函式的等價類，其中兩個函式是等價的如果它們幾乎處處相等，那么弱導數是唯一的。

此外，如果u是可微的，那么它的弱導數與導數相同。因此弱導數是導數的推廣。更進一步，兩個函式的和與積的導數公式對弱導數也是成立的。