基本介紹
- 中文名:次微分
- 外文名:subdifferential
- 領域:數學
定義
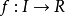



例子
概述

單元素集合
- 上述說明所有單元素集合S都是集合範疇的終對象。該範疇中沒有其它終對象。
性質
- 凸函式在x0可導,若且唯若次微分只由一個點組成,這個點就是函式在x0的導數。
- 點x0是凸函式f的最小值,若且唯若次微分中包含零,也就是說,在上面的圖中,我們可以作一條水平的“次切線”。這個性質是“可導函式在極小值的導數是零”的事實的推廣。
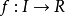
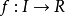




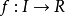
次導數(subderivative)、次微分(subdifferential)、次切線(subtangent lines)和次梯度(subgradient)的概念出現在凸分析,也就是凸函式的研究中。 要注意的是,次切線...
二階以及二階以上的微分統稱為高階微分。二階微分:若dy=f'(x)dx可微時,稱它的微分d(dy)為y的二階微分,當二階微分可微時,稱它的微分為三階微分,一般的...
對於一元函式來說,如果在該方程中出現因變數的二階導數,我們就稱為二階(常)微分方程,其一般形式為F(x,y,y',y'')=0。在有些情況下,可以通過適當的變數...
高階弗雷歇微分亦稱高階強微分,簡稱高階F微分或高階微分,是 F 微分概念的高階推廣形式。...
微分方程指含有未知函式及其導數的關係式。解微分方程就是找出未知函式。微分方程是伴隨著微積分學一起發展起來的。微積分學的奠基人Newton和Leibniz的著作中都處理過...
微分學,是指研究函式的導數與微分及其在函式研究中的套用。微分學與積分學聯繫密切,共同組成分析學的一個基本分支──微積分學。...
形如y'=f(y/x)的一階微分方程,稱為齊次一階微分方程。齊次微分方程是一個微分方程,如果它的一個解乘以任意常數後,仍是它的解,則稱為齊次微分方程。對一階...
高階微分方程是含有未知函式的導數高於一階的微分方程。求解方程高階微分方程的重要的方法就是降階法。...
數字微分器,是指執行微分運算的數字方式。整數階數字微分器用於確定和估計給定信號的(一般是關於時間)導數是十分有用的工具。微分運算是許多物理系統和計算系統中常用...
《變分分析與廣義微分1:基礎理論》是2011年科學出版社有限責任公司出版的圖書,作者是趙亞莉。...
線性微分方程組(first order linear differentialequation system)是由幾個微分方程聯立起來共同確定幾個具有同一自變數的函式的情形.這些聯立的微分方程稱為微分方程組...
《常微分方程教程(第2版)》是作者在北京大學數學學院多年教學實踐的基礎上編寫而成的,第一版於1991年出版。作者在第二版準備的過程中,在力求保持原有風格、...
《分數階偏微分方程及其數值解》 是2011年科學出版社出版的圖書,作者是郭柏靈、蒲學科、黃鳳輝。本書涵蓋了該領域的一些前沿結果以及作者目前的一些研究結果。...
一般常微分方程有各種不同的形式:有一元高階的,其中又有自治的(方程中不顯含時間)和非自治的(方程中顯含時間)之分,又有多元的常微分方程組。但是所有常見的...
次導數、次切線和次微分的概念出現在凸分析,也就是凸函式的研究中。設f:I→R是一個實變數凸函式,定義在實數軸上的開區間內。這種函式不一定是處處可導的,...
早年從事常微分方程定性理論研究,在1979年得到“二次微分系統至少存在四個極限環”的結果,指出了前蘇聯一著名數學家的“二次微分系統至多有三個極限環”的結論是錯...
拉普拉斯運算元(Laplace Operator)是n維歐幾里德空間中的一個二階微分運算元,定義為梯度(▽f)的散度(▽·f)。拉普拉斯運算元也可以推廣為定義在黎曼流形上的橢圓型運算元,...
本書共分8章,內容包括函式、極限與連續、一元函式微分學、一元函式積分學、微分方程、空間解析幾何與向量代數、多元函式微積分學及其套用、多元函式積分學、無窮...
本書共11章,主要內容包括: 函式的極限與連續、導數與微分、微分中值定理與導數的套用、不定積分、定積分及其套用、微分方程、空間解析幾何簡介、多元函式微分學及其...
習題27.3 高階可降階類型的微分方程7.3.1 不顯含y的方程7.3.2 不顯含X的方程7.3.3 m次齊次方程習題37.4 微分方程的簡單套用...
