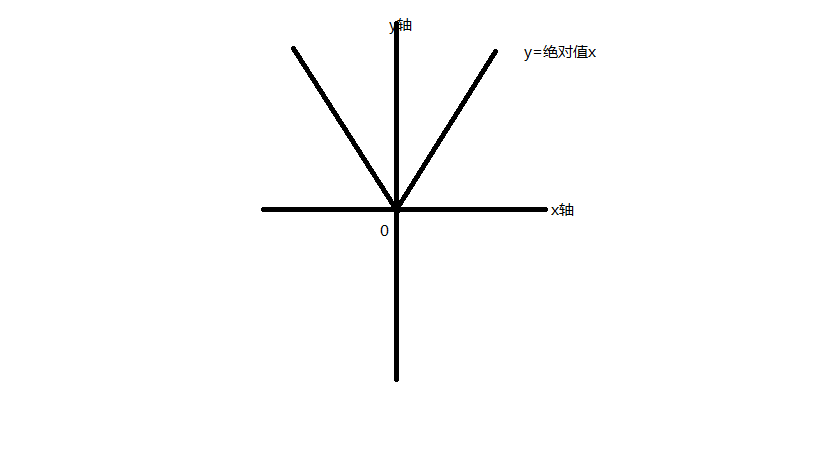
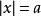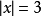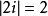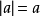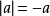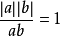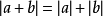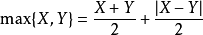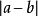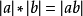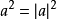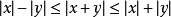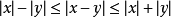意義
幾何意義
在
數軸上,一個數到
原點的距離叫做該數的絕對值。
表示數軸上表示a的點和表示b的點的距離。
套用:|5|指在數軸上5與原點的距離,這個距離是5,所以5的絕對值是5。同樣,
指在數軸上表示-5與原點的距離,這個距離是5,所以-5的絕對值也是5。
指數軸上-3和-2點的距離,這個式子值是1。同樣
也表示3和2點的距離。
 絕對值
絕對值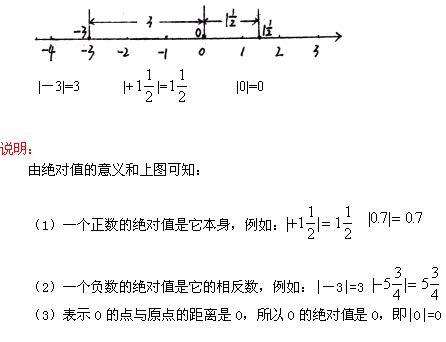 絕對值
絕對值代數意義
實數a的絕對值永遠是非負數,即
。互為相反數的兩個數的絕對值相等,即
(因為在
數軸上它們到原點的距離相等)。
套用舉例
正數的絕對值是它本身;
負數的絕對值是它的相反數;0的絕對值還是0。特殊的零的絕對值既是它的本身又是它的相反數,寫作
。
任何有理數的絕對值都是非負數,也就是說任何有理數的絕對值都大於等於0。
兩個負數比較大小,絕對值大的反而小。
計算機語言
計算機語言中,正數的
二進制首位(即符號位)為0,負數的二進制首位為1。
32位系統下,4位元組數,求絕對值的函式為abs(x)。
無論是絕對值的代數意義還是幾何意義,都揭示了絕對值的以下有關性質:
(1)任何有理數的絕對值都是大於或等於0的數,這是絕對值的非負性。
(2)絕對值等於0的數只有一個,就是0。
(3)絕對值等於同一個正數的數有兩種,這兩個數
互為相反數或相等。
(4)互為相反數的兩個數的絕對值相等。
(5)正數的絕對值是它本身。
(6)負數的絕對值是它的相反數。
(7)0的絕對值是0。
絕對值等式、不等式:
(1)若
,則
(2)
(3)
(4)
這個性質一般用在含絕對值的
一元二次方程中。
(5)
由此可以得出推論
,因為
絕對值不等式
(1)解
絕對值不等式必須設法化去式中的
絕對值符號,轉化為一般代數式類型來解;
(2)證明絕對值不等式主要有兩種方法:
A)去掉絕對值符號轉化為一般的不等式證明:
換元法、
討論法、平方法;
B)利用不等式:
,用這個方法要對絕對值內的式子進行
分拆組合、添項減項、使要證的式子與已知的式子聯繫起來。
無符號數計算
如果把三個女性記為-3,把四個男性記為+4,問有幾個人,計算方法是兩個數的絕對值相加,也就是7個人。如果問男女差是多少,計算方法是相對數相加,是+1。
如果把向南走1公里記為+1,把向北走2公里記為-2,問走了多少公里,計算方法是兩個數的絕對值相加,也就是3公里。如果問相對走了多少公里,計算方法是相對數相加,是-1。
如果把向零上的10度記為+10,把零下5度記為-5,上下差多少度,計算方法是兩個數的絕對值相加,也就是15度。如果問溫的和是多少度,計算方法就是
相對數相加,是+5。
如果題中沒有說什麼是正,如:郵遞員送信先向南10米,再向北5米,做題前必須寫:記什麼為正,一般不用寫另一個,因為不是正就是負,知道一個就行了。
所以對於絕對值的概念也是有爭議的。有人並不認為絕對值就一定是正數。這說明數學也是在不斷發展之中的。而我們的見到的數學只是歷史的過程中的一個階段之一,沒有影響到正常的學習。
求兩個數的最大值
利用絕對值可以求兩個數中的最大值,公式如下:

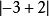
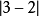
 絕對值
絕對值 絕對值
絕對值