範數(norm)是數學中的一種基本概念。在泛函分析中,它定義在賦范線性空間中,並滿足一定的條件,即①非負性;②齊次性;③三角不等式。它常常被用來度量某個向量空間(或矩陣)中的每個向量的長度或大小。
基本介紹
- 中文名:範數
- 外文名:norm
- 套用學科:數學
- 適用領域範圍:代數
- 本質:函式
- 滿足條件:非負性,齊次性,三角不等式
- 作用:大小 長度的度量
名詞定義






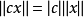













運算元範數




空間範數
基本性質
常用範數



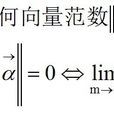
範數(norm)是數學中的一種基本概念。在泛函分析中,它定義在賦范線性空間中,並滿足一定的條件,即①非負性;②齊次性;③三角不等式。它常常被用來度量某個向量空間(或矩陣)中的每個向量的長度或大小。






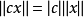




















範數(norm)是數學中的一種基本概念。在泛函分析中,它定義在賦范線性空間中,並滿足一定的條件,即①非負性;②齊次性;③三角不等式。它常常被用來度量某個向量...
二範數指矩陣A的2範數,就是A的轉置共軛矩陣與矩陣A的積的最大特徵根的平方根值,是指空間上兩個向量矩陣的直線距離。類似於求棋盤上兩點間的直線距離。...
矩陣範數(matrix norm)是數學中矩陣論、線性代數、泛函分析等領域中常見的基本概念,是將一定的矩陣空間建立為賦范向量空間時為矩陣裝備的範數。套用中常將有限維賦...
準範數(paranorm)是範數的又一種推廣。準範數是定義線上性空間X上,並且滿足一定條件的實值函式。賦范線性空間一定是賦準范線性空間。...
L1範數正則化( L1 regularization 或 lasso )是機器學習(machine learning)中重要的手段,在支持向量機(support vector machine)學習過程中,實際是一種對於成本函式(...
等價範數(equivalence of norms)是同一個線性空間上的兩個範數之間的一種關係。有限維空間上的任何兩個範數必是等價的,且具有相同維數的兩個有窮維線性賦范空間...
C2類運算元稱為希爾伯特-施密特運算元,而相應的範數‖·‖2稱為希爾伯特-施密特範數。...... C2類運算元稱為希爾伯特-施密特運算元,而相應的範數‖·‖2稱為希爾伯特-施密特...
運算元範數(operate norm)是矩陣範數的一種。...... 運算元範數是矩陣範數的一種,設向量x是一個n維向量,A是一個n*n的矩陣,則A的運算元範數為Max(Ax/x).運算元範數...
最小範數解(minimum norm)是概周期解存在性的一個重要概念。線性微分方程論對常係數非齊次。...
範數不等式是一種在有效實用的不等式,又稱反向柯西不等式。...... 範數不等式編輯 鎖定 範數不等式是一種在有效實用的不等式,又稱反向柯西不等式。...
三角範數亦稱t範數,是一種定義在正方形上在單位閉區間中取值的具有特殊性質的函式。...
BMO範數(BMO norm)記為||f||∗,其中,BMO是有界平均振動之意。...... BMO範數(BMO norm)記為||f||∗,其中,BMO是有界平均振動之意。中文名 BMO範數 ...
在通常的套用中,例如在函式空間中,它們有一個代數結構,即構成一個線性空間,同時還與某種收斂性相聯繫,處理這種結構最常用的一般方法是引入一個範數,這樣就導致賦...
如果其對於這個範數來說是完備的,此空間稱為是一個希爾伯特空間。這裡的完備性是指,任何一個柯西序列都收斂到此空間中的某個元素,即它們與某個元素的範數差的...
數學定義為矩陣A的條件數等於A的範數與A的逆的範數的乘積,即cond(A)=‖A‖·‖A的逆‖,對應矩陣的3種範數,相應地可以定義3種條件數。...
在數學中,歐幾里得距離或歐幾里得度量是歐幾里得空間中兩點間“普通”(即直線)距離。使用這個距離,歐氏空間成為度量空間。相關聯的範數稱為歐幾里得範數。較早的文獻稱...
格式:n=norm(A,p) 功能:norm函式可計算幾種不同類型的矩陣範數,根據p的不同可得到不同的範數...
將 矩陣按照列的形式,排成一個 的向量,然後採用向量範數的定義,即得到矩陣的元素形式範數 [25] ,表式如下:矩陣Schatten範數 Schatten範數是用矩陣的奇異值定義的...
H∞最優控制,簡而言之,就是用H∞範數作為日標函式的度量邊行最佳化設計。H∞範數是定義在Hardy空間 上的範數,在H∞控制理論中是指在S右半平面上解析的有理函式...
