基本介紹
- 外文名:normed space
定義


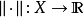
1)對



2)對


3)對

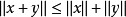
稱





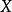
範數誘導的距離
強(或按范)收斂


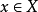

稱



或

Banach空間
性質
性質1


性質2



當



性質3



收斂,則級數


反之,如果在一個賦范空間中,任意無窮級數


拓撲結構





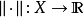






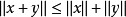





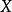


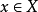























在通常的套用中,例如在函式空間中,它們有一個代數結構,即構成一個線性空間,同時還與某種收斂性相聯繫,處理這種結構最常用的一般方法是引入一個範數,這樣就導致賦...
賦范線性空間(normed linear space)是線上性空間中引進一種與代數運算相聯繫的度量,即由向量範數誘導出的度量。賦范線性空間稱為Banach空間,是指由範數導出的度量...
一個賦有擬範數的向量空間被稱為擬賦范向量空間。一個完備擬賦范向量空間被稱為擬巴拿赫空間。一個擬賦范空間{\displaystyle (A,\|\cdot \|)}被稱為擬賦...
模糊賦范空間(fuzzy normed space)是賦范空間的一種推廣,它是一類特殊的模糊拓撲線性空間。模糊賦范空間的概念是吳從炘、方錦暄於1984年給出的,同年,凱茲拉斯(A...
商賦范線性空間是由賦范線性空間與其閉子空間誘導出的新的賦范線性空間。...... 商賦范線性空間是由賦范線性空間與其閉子空間誘導出的新的賦范線性空間。...
賦準范線性空間(paranormed linear space)又稱為賦擬范線性空間,簡稱賦準范空間。...... 賦準范線性空間(paranormed linear space)又稱為賦擬范線性空間,簡稱賦...
賦范線性空間是一類可以引進“長度”概念的線性空間。 一致凸賦范線性空間(uniformly convexnormed linear space)是滿足一致凸性的一類賦范線性空間。 [1] 中文...
是一個半範數,取幾乎處處為0,則關於的商空間是一個賦范向量空間,記作。一致範數與p-範數之間存在以下關係:可以證明,L空間是完備的空間,也即是說是一個巴拿赫...
嚴格凸賦范線性空間(strictly convex normed linear space)是滿足嚴格凸性的一類賦范線性空間,簡稱為嚴格凸空間,常用於討論最佳逼近元的唯一性,以及有界線性泛函保...
超自反巴拿赫空間(super-reflexive Banach space)屬於一類自反空間,是具有超自反性的巴拿赫空間。每個在X中有有限表示的巴拿赫空間Y都是自反的。巴拿赫空間(含賦范...
,則在‖0‖下,H構成一個線性賦范空間。完備的內積空間稱為希爾伯特空間,希爾伯特空間的概念還可以推廣到複線性空間上。歐幾里德空間是希爾伯特空間的一個重要特例,...
學位級別 d 1989n 學位授予單位 哈爾濱工業大學 學位授予時間 1989 關鍵字 賦范空間理論 館藏號 O177 唯一標識符 108.ndlc.2.1100009031010001/T3F24....
這時(·,·)稱為H中的內積,而稱H為(實或復)內積空間,或準希爾伯特空間.令‖x‖= ,則按範數‖·‖,H成為賦范線性空間.設(X,‖·‖)是賦范線性空間,X...
數學上,一個索伯列夫空間是一個由函式組成的賦范向量空間,對於某個給定的p≥ 1,它對一個函式f和它的直到某個k階導數加上有限Lp範數的這個條件。它以前蘇聯...
平性凸賦范線性空間(flat convex normed linear space)是一類賦范線性空間。...... 平性凸賦范線性空間(flat convex normed linear space)是一類賦范線性空間。...
在數學裡,尤其是在泛函分析之中,巴拿赫空間是一個完備賦范向量空間。更精確地說,巴拿赫空間是一個具有範數並對此範數完備的向量空間。...
關於N的商空間。 中的某個元素f可以看作是所有和函式f相差一個N中元素的函式構成的等價類。這樣定義的空間 是一個賦范向量空間,稱為S上函式關於測度μ的L空間...
這樣定義的空間 是一個賦范向量空間,稱為S上函式關於測度μ的L空間。 稱為 函式的p-範數。需要注意的是,L空間中的元素嚴格來說並不是具體的函式,而是一族函式...
賦范向量格,即賦范向量空間。在數學中,賦范向量空間是具有“長度”概念的向量空間。...
索伯列夫空間是數學裡由函式組成的賦范向量空間,主要用來研究偏微分方程理論,它以前蘇聯數學家С.Л.索伯列夫命名。...
範數(norm)是數學中的一種基本概念。在泛函分析中,它定義在賦范線性空間中,並滿足一定的條件,即①非負性;②齊次性;③三角不等式。它常常被用來度量某個向量...
