介紹
在古代,當
算術里積累了大量的,關於各種數量問題的解法後,為了尋求有系統的、更普遍的方法,以解決各種
數量關係的問題,就產生了以解
代數方程的原理為中心問題的
初等代數。
代數(algebra)是由算術(arithmetic)演變來的,這是毫無疑問的。至於什麼年代產生的
代數學這門學科,就很不容易說清楚了。比如,如果你認為“代數學”是指解bx+k=0這類用符號表示的代數方程的技巧。這種“代數學”是在十六世紀才發展起來的。
定義
代數是數學的一個分支。傳統的代數用有字元 (變數) 的表達式進行算術運算,字元代表未知數或未定數。如果不包括除法 (用整數除除外),則每一個表達式都是一個含有理係數的多項式。例如: 1/2 xy +1/4z-3x+2/3. 一個代數方程式 (參見EQUATION)是通過使多項式等於零來表示對變數所加的條件。如果只有一個變數,那么滿足這一方程式的將是一定數量的實數或複數——它的根。一個代數數是某一方程式的根。代數數的理論——
伽羅瓦理論是數學中最令人滿意的分支之一。建立這個理論的
伽羅瓦(Evariste Galois,1811-32)在21歲時死於決鬥中。他證明了不可能有解五次方程的代數公式。用他的方法也證明了用直尺和圓規不能解決某些著名的幾何問題(立方加倍,三等分一個角)。多於一個變數的代數方程理論屬於代數幾何學,抽象代數學處理廣義的數學結構,它們與算術運算有類似之處。參見,如:
布爾代數(BOOLEAN ALGEBRA);
群 (GRO-UPS);
矩陣(MATRICES);
四元數(QUA-TERNIONS );
向量(VECTORS)。這些結構以公理 (見公理法 AXIOMATICMETHOD) 為特徵。特別重要的是結合律和交換律。代數方法使問題的求解簡化為符號表達式的操作,已滲入數學的各分支。
設K為一交換體. 把K上的向量空間E叫做K上的代數,或叫K-代數,如果賦以從E×E到E中的雙線性映射.換言之,賦以集合E由如下三個給定的法則所定義的代數結構:
——記為加法的合成法則(x,y)↦x+y;
——記為乘法的第二個合成法則(x,y)↦xy;
——記為乘法的從K×E到E中的映射(α,x)↦αx,這是一個作用法則;
這三個法則滿足下列條件:
a) 賦以第一個和第三個法則,E則為K上的一個向量空間;
b) 對E的元素的任意三元組(x,y,z),有
x(y+z)=xy+xz(y+z)x=yx+zx;
c)對K的任一元素偶(α,β)及對E的任一元素偶(x,y),有(αx)(βy)=(αβ) (xy).
設A為一非空集合. 賦予從A到K中的全體映射之集ℱ(A,K)以如下三個法則:
則ℱ(A, K)是K上的代數, 自然地被稱為從A到K中的映射代數.當A=N時, 代數ℱ(A,K)叫做K的元素序列代數.
無論是在代數還是在分析中,代數結構都是最常見到的結構之一。十九世紀前半葉末,隨著哈密頓四元數理論的建立,非交換代數的研究已經開始. 在十九世紀下半葉,隨著M.S.李的工作,非結合代數出現了. 到二十世紀初,由於放棄實數體或複數體作為運算元域的限制,代數得到了重大擴展.
溯源
如果我們對代數符號不是要求像現在這樣簡練,那么,
代數學的產生可上溯到更早的年代。
 古希臘數學家丟番圖
古希臘數學家丟番圖西方人將公元前三世紀古希臘數學家
丟番圖看作是代數學的鼻祖,而真正創立代數的則是古
阿拉伯帝國時期的偉大數學家默罕默德·伊本·穆薩(我國稱為“花剌子密”,生卒約為公元780-850年)。而在中國,用文字來表達的代數問題出現的就更早了。
“代數”作為一個數學專有名詞、代表一門數學分支在我國正式使用,最早是在1859年。那年,清代數學家
李善蘭和英國人韋列亞力共同翻譯了英國人棣么甘所寫的一本書,譯本的名稱就叫做《代數學》。當然,代數的內容和方法,我國古代早就產生了,比如《
九章算術》中就有方程問題。
代數的起源可以追溯到古
巴比倫的時代[1],當時的人們發展出了較之前更進步的算術系統,使其能以代數的方法來做計算。經由此系統地被使用,他們能夠列出含有未知數的方程並求解,這些問題在今日一般是使用
線性方程、
二次方程和不定線性方程等方法來解答的。相對地,這一時期大多數的
埃及人及西元前1世紀大多數的印度、希臘和中國等數學家則一般是以幾何方法來解答此類問題的,如在蘭德數學紙草書、繩法經、
幾何原本及
九章算術等書中所描述的一般。希臘在幾何上的工作,以幾何原本為其經典,提供了一個將解特定問題解答的公式廣義化成描述及解答代數方程之更一般的系統之架構。
代數(algebra)導源於阿拉伯語單字“al-jabr”,其出自 al-Kitāb al-muḫtaṣar fī ḥisāb al-ğabr wa-l-muqābala這本書的書名上,意指移項和合併同類項之計算的摘要,其為波斯回教數學家
花拉子米於820年所著。Al-Jabr此詞的意思為“重聚”。傳統上,希臘數學家
丟番圖被認為是“代數之父”,的成果到今日都還有用途,且他更給出了一個解答二次方程的一詳盡說明。而支持丟番圖的人則主張在Al-Jabr里出現的代數比在Arithmetical里出現的更為基本,且Arithmetical是簡字的而Al-Jabr卻完全是文辭的。[3]另一位波斯數學家
歐瑪爾·海亞姆發展出
代數幾何出,且找出了
三次方程的一般幾何解法。印度數學家摩訶吠羅和
婆什迦羅與中國數學家
朱世傑解出了許多三次、四次、五次及更高次
多項式方程的解了。
代數更進一步發展的另一個關鍵事件在於三次及四次方程的一般代數解,其發展於16世紀中葉。
行列式的概念發展於17世紀的日本數學家
關孝和手中,並於十年後由
萊布尼茨繼續發展著,其目的是為了以
矩陣來解出線性方程組的答案來。
加布里爾·克拉默也在18世紀時在矩陣和行列式上做了一樣的工作。
抽象代數的發展始於19世紀,一開始專注在今日稱為
伽羅瓦理論及
規矩數的問題上。
組成
初等代數
在古代,當
算術里積累了大量的,關於各種數量問題的解法後,為了尋求有系統的、更普遍的方法,以解決各種
數量關係的問題,就產生了以解
代數方程的原理為中心問題的
初等代數。
 初等的代數運算
初等的代數運算初等代數(elementary algebra)是研究數字和文字的
代數運算理論和方法,更確切的說,是研究實數和
複數,以及以它們為係數的代數式的代數運算理論和方法的數學分支
學科。
用通俗的語言解釋什麼是初等代數,就是說:如果我們將算術定義為分別研究蘋果、梨、橘子、葡萄等各有什麼特點,那么初等代數就是研究水果的共性。
初等代數的基本內容如下
值得注意的是:根據方程的定義,只要是含有
未知數的
等式,就是方程。這裡之所以要強調”
代數方程“,是因為除了代數方程之外,還有
超越方程(即非代數的初等方程,包括
指數方程、
對數方程、
三角方程、反三角方程等)、
微分方程、
差分方程、
積分方程等許多其他形式的方程。後面幾類顯然不屬於代數的範疇。一些有關數學史的內容經常將代數定義為“以
解方程為核心的學科”,主要是因為歷史上關於代數方程的知識在微積分等
近代數學分支建立以前就早有研究了。既然當時都沒有
微積分,數學家們又怎能想起建立
微分方程的概念呢?
初等代數(elementary algebra)的內容大體上相當於現行中學設定的代數課程的內容,但又不完全相同。比如,嚴格的說,數的概念、排列和組合應歸入算術的內容;函式是分析數學的內容;
不等式的解法有點像
解方程的方法,但不等式作為一種估算數值的方法,本質上是屬於
分析數學的範圍;坐標法是研究解析幾何的,等等。這些都只是歷史上形成的一種編排方法。
初等代數是算術的繼續和推廣,初等代數研究的對象是
代數式的運算和代數方程的求解。
代數運算的特點是只進行有限次的加、減、乘、除和開方。全部初等代數總起來有十條規則。這是學習初等代數需要理解並掌握的要點。
規則
兩條等式基本性質:等式兩邊同時加(減)上一個數,等式不變;等式兩邊同時乘(除)以一個非零的數,等式不變;
初等代數學進一步地向兩個方面發展,一方面是研究未知數更多的一次方程組;另一方面是研究未知數次數更高的(一元)
高次方程。這時候,代數學已由初等代數向著
高等代數的方向發展了,相應地也形成了”
線性代數“與”(一元)
多項式代數“兩大板塊。
1° a-b=0,若且唯若a=b;
2° a+b=0,若且唯若a=-b,或者b=-a;
3° a·b=0,若且唯若a=0,或b=0;
4° (a-b) 2=0,若且唯若a=b。
高等代數
研究對象
高等代數是
代數學發展到高級階段的總稱,它包括許多分支。大學裡開設的高等代數,一般包括兩部分:
線性代數、多項式代數。
高等代數在初等代數的基礎上研究對象進一步的擴充,引進了許多新的概念以及與通常很不相同的量,比如最基本的有集合、
向量和
向量空間等。這些量具有和數相類似的運算的特點,不過研究的方法和運算的方法都更加繁複。集合是具有某種屬性的事物的全體;向量是除了具有數值還同時具有方向的量;向量空間也叫線性空間,是由許多向量組成的並且符合某些特定運算的規則的集合。向量空間中的運算對象已經不只是數,而是向量了,其運算性質也有很大的不同了。
與線性代數的區別和聯繫
高等代數是大學數學專業開設的專業課,線性代數是大學中除了數學專業以外的理科、工科和部分醫科專業開設的課程。
解代數方程
 複雜的運算
複雜的運算初等代數的中心內容是解
代數方程,因而長期以來都把代數學理解成代數方程的科學,數學家們也把主要精力集中在代數方程的研究上。它的研究方法是高度計算性的。
要討論代數方程,首先遇到的一個問題是如何把實際中的數量關係組成
代數式,然後根據
等量關係列出方程。所以初等代數的一個重要內容就是代數式。由於事物中的數量關係的不同,大體上初等代數形成了
整式、
分式和
根式這三大類代數式。代數式是數的化身,因而在代數中,它們都可以進行
四則運算,服從
基本運算定律,而且還可以進行
乘方(這裡僅限於有理數指數冪)和開方兩種新的運算。通常把這六種運算叫做
代數運算,以區別於只包含四種運算的
算術運算。
在初等代數的產生和發展的過程中,通過
代數方程的研究,也促進了數的概念的進一步發展,將算術中討論的整數和分數的概念擴充到有理數的範圍,使數包括正負整數、正負分數和零。這是初等代數的又一重要內容,就是數的概念的擴充。
有了有理數,初等代數能解決的問題就大大的擴充了。但是,有些一元多項式方程在有理數範圍內仍然沒有解。於是,數的概念在一次擴充到了
實數,進而又進一步擴充到了
複數。
那么到了複數範圍內是不是仍然有代數方程沒有解,還必須把複數再進行擴展呢?數學家們說:不用了。這就是代數裡的一個著名的定理——
代數基本定理。這個定理簡單地說就是
n次方程有
n個根。1742年12月15日瑞士數學家
歐拉曾在一封信中明確地做了陳述,後來另一個數學家、德國的
高斯在1799年給出了嚴格的證明。
詞的起源
代數學的英文名稱algebra來源於9世紀阿拉伯數學家花拉子米的重要著作的名稱。該著作名為“ilm al-jabr wa'1 muqabalah”,原意是“還原與對消的科學”。這本書傳到歐洲後,簡譯為algebra。清初曾傳入中國兩卷無作者的代數學書,被譯為《阿爾熱巴拉新法》,後改譯為《代數學》。
交換環的代數
在數學中,交換環上的代數或多元環是一種
代數結構,上下文不致混淆時通常徑稱代數。
定義
設R為一交換環,R上的代數(或稱A-代數)是下述結構:
r(a*b)=(ra)*b=a*(rb)對任何
成立
最常考慮的情形是R是一個域,這時稱域代數,一些作者也將代數定義成域上的代數。
若
A上的乘法滿足交換性ab=ba,則稱之為
可交換代數;若
A上的乘法滿足
結合律a(bc)=(ab)c,則稱之為“結合代數”,詳見
結合代數詞條。
交換代數學中考慮的代數均屬可交換的結合代數。
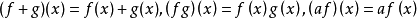
 古希臘數學家丟番圖
古希臘數學家丟番圖 複雜的運算
複雜的運算
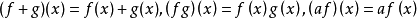
 古希臘數學家丟番圖
古希臘數學家丟番圖 複雜的運算
複雜的運算