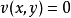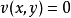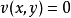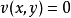基本介紹
- 中文名：代數基本定理
- 外文名：fundamental theorem of algebra
- 分類：數學
- 證明：高斯
- 時間：1799年
- 提出：洛特
簡介,證明歷史,證明方法,複分析證明,拓撲學證明,代數證明,
簡介
有時這個定理表述為：任何一個非零的一元n次復係數多項式，都正好有n個複數根。這似乎是一個更強的命題，但實際上是“至少有一個根”的直接結果，因為有一個根xa，只要不斷把多項式除以(x-xa)，即可從有一個根推出有n個根。
儘管這個定理被命名為“代數基本定理”，但它還沒有純粹的代數證明，許多數學家都相信這種證明不存在。另外，它也不是最基本的代數定理；因為在那個時候，代數基本上就是關於解實係數或復係數多項式方程，所以才被命名為代數基本定理。
證明歷史
代數基本定理在代數乃至整個數學中起著基礎作用。 最早該定理由德國數學家羅特於1608年提出。據說，關於代數學基本定理的證明，現有200多種證法。 迄今為止，該定理尚無純代數方法的證明。大數學家 J.P. 塞爾 曾經指出：代數基本定理的所有證明本質上都是拓撲的。 美國數學家John Willard Milnor在數學名著《從微分觀點看拓撲》一書中給了一個幾何直觀的證明，但是其中用到了和臨界點測度有關的sard定理。 複變函數論中，對代數基本定理的證明是相當優美的，其中用到了很多經典的複變函數的理論結果。
代數基本定理的第一個嚴格證明通常認為是高斯給出的(1799年在哥廷根大學的博士論文)，基本思想如下：
設
為n次實係數多項式，記
，考慮方根：
即
與
這裡與分別表示oxy坐標平面上的兩條曲線C1、C2，於是通過對曲線作定性的研究，他證明了這兩條曲線必有一個交點
，從而得出
，即
，因此z0便是方程
的一個根，這個論證具有高度的創造性，但從現代的標準看依然是不嚴格的，因為他依靠了曲線的圖形，證明它們必然相交，而這些圖形是比較複雜，正中隱含了很多需要驗證的拓撲結論等等。
高斯後來又給出了另外三個證法，其中第四個證法是他71歲公布的，並且在這個證明中他允許多項式的係數是複數。
證明方法
定理的某些證明僅僅證明了任何實係數多項式都有複數根。這足以推出定理的一般形式，這是因為，給定復係數多項式p(z)，以下的多項式
就是一個實係數多項式，如果z是q(z)的根，那么z或它的共軛複數就是p(z)的根。
許多非代數證明都用到了“增長引理”：當|z|足夠大時，首係數為1的n次多項式函式p(z)的表現如同z。一個更確切的表述是：存在某個正實數R，使得當|z| > R時，就有：
複分析證明
證明一
尋找一個中心為原點，半徑為r的閉圓盤D，使得當|z| ≥ r時，就有|p(z)| > |p(0)|。因此，|p(z)|在D內的最小值（一定存在，因為D是緊緻的），是在D的內部的某個點z0取得，但不能在邊界上取得。於是，根據最小模原理，p(z0) = 0。也就是說，z0是p(z)的一個零點（根）。
證明二
由於在D之外，有|p(z)| > |p(0)|，因此在整個複平面上，|p(z)|的最小值在z0取得。如果|p(z0)| > 0，那么1/p在整個複平面上是有界的全純函式，這是因為對於每一個複數z，都有|1/p(z)| ≤ |1/p(z0)|。利用劉維爾定理（有界的整函式一定是常數），可知1/p是常數，因此p是常數。於是得出矛盾，所以p(z0) = 0。
證明三
這個證明用到了輻角原理。設R為足夠大的正實數，使得p(z)的每一個根的絕對值都小於R；這個數一定存在，因為n次多項式函式最多有n個根。對於每一個r > R，考慮以下的數：
其中c(r)是中心為0，半徑為r的逆時針方向的圓；於是輻角原理表明，這個數是p(z)在中心為0、半徑為r的開圓盤內的零點的數目N，由於r > R，所以它也是p(z)的零點的總數目。另一方面，n/z沿著c(r)的積分除以2πi，等於n。但這兩個數的差為：
被積分的有理表達式中的分子，次數最多是n 1，而分母的次數是n + 1。因此，當r趨於+∞時，以上的數趨於0。但這個數也等於N n，因此有N = n。
證明四
設A為大小n > 0的方塊矩陣，並設In為相同大小的單位矩陣。假設A沒有特徵值。考慮預解函式
另一方面，把R(z)展開為幾何級數，可得：
這個公式在半徑為||A||的閉圓盤的外部（A的運算元範數）成立。設r > ||A||。那么：
（僅當k = 0時，積分才不等於零）。於是得出矛盾，因此A一定有一個特徵值。
拓撲學證明
設
為使|p(z)|在
取得最小值的數; 從用到劉維爾定理的證明中，可以看到這樣一個數一定存在。我們可以把p(z)寫成z z0的多項式：存在某個自然數k和一些複數
，使得
，以及：
可推出如果a是
的一個k重根，且t是足夠小的正數，那么|p(z0 + ta)| < |p(z0)|，這是不可能的，因為|p(z0)|是|p|在D內的最小值。
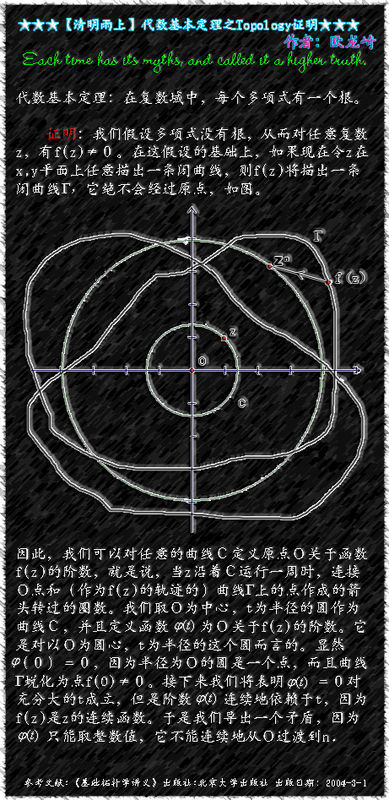
對於另外一個用到反證法的拓撲學證明，假設p(z)沒有根。選擇一個足夠大的正數R，使得對於|z| = R，p(z)的第一項z大於所有其它的項的和；也就是說，|z| > |an 1z + ··· + a0|。當z依逆時針方向繞過方程為|z| = R的圓一次時，p(z)，像z那樣，依逆時針方向繞過零n次。在另外一個極端，|z| = 0時，“曲線” p(z)僅僅是一個（非零的）點p(0)，它的卷繞數顯然是0。如果z所經過的迴路在這兩個極端中被連續變形，那么p(z)的路徑也連續變形。我們可以把這個變形記為
，其中t大於或等於0，而小於或等於1。如果我們把變數t視為時間，那么在時間為零時，曲線為p(z)，時間為1時，曲線為p(0)。顯然在每一個點t，根據原先的假設p(z)都不能是零，因此在變形的過程中，曲線一直都沒有經過零。因此曲線關於0的繞數應該不變。然而，由於繞數在一開始是n，結束時是0，因此得出矛盾。所以，p(z)至少有一個根。
