基本介紹
- 中文名:伽羅瓦擴張
- 外文名:galois extension
- 領域:數學
- 相關:正規擴張又是可分擴
- 類型:名詞
- 屬於:伽羅瓦理論的核心概念
定義
等價定義
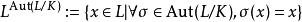
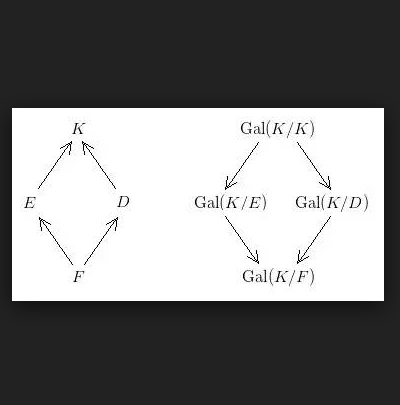
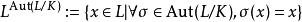
伽羅瓦擴張:在數學中,如果一個域擴張 K/k 既是一個正規擴張又是可分擴張,那 K/k 就是一個伽羅瓦擴張。注意正規擴張隱含了 K/k 是一個代數擴張。...
伽羅瓦理論基本定理是抽象代數中的定理,通過群的概念來描述特定域擴張的細緻結構。...... 域擴張L/K是有限伽羅瓦擴張 伽羅瓦理論基本定理說明了,如果某個域擴張L/K...
循環擴張(cyclic extension)是一類特殊的、結構較清楚的域擴張。設K是域F的有限次伽羅瓦擴域,若其伽羅瓦群G(K/F)為循環群,則稱此域擴張為循環擴張,K/F為循環...
伽羅瓦預解式(Galois resolvent),是決定方程的伽羅瓦群的一個函式式。伽羅瓦(Galois,Evariste),法國數學家。法國數學家。他發現每個代數方程必有反映其特性的置換群...
域擴張(field extensions)是數學分支抽象代數之域論中的主要研究對象,基本想法是從一個基域開始以某種方式構造包含它的“更大”的域。域擴張可以推廣為環擴張。...
滿足這些條件的F的擴域K稱為F的一個伽羅瓦擴域,K/F稱為伽羅瓦擴張,GK(F)=G(K/F)稱為K/F的伽羅瓦解。K是F上的有限次伽羅瓦擴域若且唯若K是F上一切可...
分解群是伽羅瓦群的一個子群,它使得這個正規擴張的某個賦值環穩定不變。分解群還是素理想分解因子的固定伽羅瓦子群。...
克魯爾拓撲(Krull topology)是一種拓撲。用以推廣有限伽羅瓦理論的基本定理。它是克魯爾(Krull,W.)於1928年對無限伽羅瓦群引入的。...
阿廷映射(Artin mapping)是理想群(或伊代爾群)到伽羅瓦群的映射。它是類域論的基石之一。伊代爾群是一種特殊的群。即各分量為諸局部域元素的某些向量(其分量幾乎...
希爾伯特分歧理論(Hilbert ramification theo-rem)擴域素分解的精細理論.設E是普通算術域F,的n次伽羅瓦擴張,伽羅瓦群為G,且設可能的剩餘類域擴張}lF'總可分.設p...
伽羅瓦擴張 參考資料 1. Lang, Serge (2002), Algebra, Graduate Texts in Mathematics, 211 (Revised third ed.), New York: Springer-Verlag, ISBN 978-0...
