希爾伯特分歧理論(Hilbert ramification theo-rem)擴域素分解的精細理論.設E是普通算術域F,的n次伽羅瓦擴張,伽羅瓦群為G,且設可能的剩餘類域擴張}lF'總可分.設p與R為F與E的素理想,月{P.以。, .f.,記R在h的分歧指數、剩餘類次數、分裂次數.於是}.f} = n.對}lF'的中間域M,記風,=R自M,M為模月、剩餘類域;對G的子群H,記}H為H的固定子域,風,一風11.記式中O:為E的整數環,yiU.子群D稱為分解群,}D稱為分解域或分裂域;I"-}(。稱為慣性群,1"7稱為慣性域;V稱為:次分歧群,三一E叭稱為:次分歧域.
希爾伯特分歧理論(Hilbert ramification theo-rem)擴域素分解的精細理論.設E是普通算術域F,的n次伽羅瓦擴張,伽羅瓦群為G,且設可能的剩餘類域擴張}lF'總可分.設p與R為F與E的素理想,月{P.以。, .f.,記R在h的分歧指數、剩餘類次數、分裂次數.於是}.f} = n.對}lF'的中間域M,記風,=R自M,M為模月、剩餘類域;對G的子群H,記}H為H的固定子域,風,一風11.記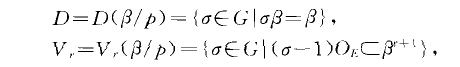
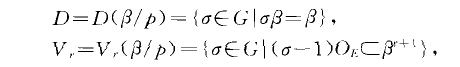
式中O:為E的整數環,yiU.子群D稱為分解群,}D稱為分解域或分裂域;I"-}(。稱為慣性群,1"7稱為慣性域;V稱為:次分歧群,三一E叭稱為:次分歧域.
