具體介紹
代數
數論主要起源於費馬大定理的研究。法國數學家P. de費馬在學習與翻譯丟番圖的《算術》一書時,在書邊上寫下了著名的"大定理",即方程x^n+y^n=z^n(n>2)沒有xyz≠0的
整數解。經過三個半世紀的努力,這個世紀數論難題才由
普林斯頓大學英國數學家安德魯·懷爾斯和他的學生理查·泰勒於1995年成功證明。證明利用了很多新的數學,包括
代數幾何中的橢圓曲線和模形式,以及伽羅華理論和Hecke代數等,令人懷疑費馬是否真的找到了正確證明。而安德魯·懷爾斯(Andrew Wiles)由於成功證明此定理,獲得了1998年的
菲爾茲獎特別獎以及2005年度
邵逸夫獎的數學獎。
 公式1
公式1容易看出,這個結果的證明,可以歸結到n=4以及n為
奇素數的情形。費馬本人給出了n=4的證明,L.歐拉與A.-M.勒讓德證明了n=3的情形,P.G.L.狄利克雷證明了n=5的情形。雖然對於許多奇素數,人們已經證明了這個結果,但始終沒有得到一個一般的證明。E.E.庫默爾是努力證明費馬大定理的數學家之一。他利用n次本原
單位根代數
數論把
方程 xn+yn=zn寫成(公式1)代數數論,他以為在分圓域代數數論中, “
整數”也象普通整數一樣,可以唯一地分解成素數的乘積。在這個前提下,庫默爾給出費馬大定理的證明。不久,他自己發現他的假定是錯誤的,即在分圓域中, “整數”分解成素數的乘積不具有唯一性。這個發現使庫默爾引入“
理想數”的概念,他隨之證明了,每個“理想數”可以唯一地分解成素因子的乘積,因而就建立了分圓域上的數論。J.W.R.戴德金把庫默爾的工作系統化並推廣到一般的代數數域,為代數
數論奠定了基礎。
 公式2
公式2 公式3
公式3 公式4
公式4C.F.高斯關於二元
二次型的深入研究也引起了二次數域
算術的研究。
有理數域Q上的有限擴張K 稱為有限次的代數數域,K 對Q 的次數n=【K:Q】就是指K作為Q上
線性空間的維數。K中每個元素都是一個次數不超過n的有理係數
多項式(公式2)的根。因為乘一非零整數後,多項式的根不變,所以不妨假定(1)是整係數多項式。如果K 中元素α使一個首項係數為1(即α0=1)的整係數多項式(1)為零,那么α就稱為一代數
整數。K 中全體代數整數組成一個具有單位元素的交換
整環OK。對於環OK中的理想A、B定義
乘法(公式3)。
 公式5
公式5即由A、B中元素之積的有限和組成的集合,顯然,AB也是OK的理想。一個理想P 稱為
素理想,就是指由αβ∈P必有α∈P或β∈P。可以證明,在代數整數環OK中,每個非零理想A都可以唯一地分解成素理想的乘積,即A=P1P2…Pt,其中Pi(i=1,2,…,t)是素理想。在通常的整數環Z中,每個理想都是由一非負整數的
倍數所組成,因之,非零理想與正整數是一一對應的。由此可見,關於理想分解的定理正是通常整數的因子分解定理的一個推廣。
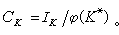 公式6
公式6OK的全體非零理想組成一
乘法半群, OK就是這個乘法半群的單位元素。為了方便,引入
分式理想的概念。如果K 的一個子集合A是一個有限生成的OK模,那么A 就稱為一分式理想。顯然,理想全是
分式理想。由K中任一元素α 的整數倍rα(r∈OK)組成的集合也是分式理想,它們稱為主分式理想。對於分式理想可以同樣地定義乘法。可以證明,K 中全體非零的分式理想在
乘法下成一群,而且每個分式理想A 都可以唯一地表成
素理想方冪的乘積(公式4)這個群稱為K的理想群,記為IK。
 公式7
公式7環OK中可逆元素稱為單位。全體單位組成一乘法群,記為UK。顯然,K 中非零元素α 生成的主理想(α)=OK的充分必要條件是α∈UK。下面的正合列是基本的(公式5)
 公式8
公式8其中K*表示K 中全體非零
元素組成的
乘法群,而φ 把K*中元素映射到它生成的主理想(公式6)CK稱為K的理想類群,其元素是理想類。按定義IK,中兩個理想A、B屬於同一類,若且唯若有α∈K*使A=αB。代數
數論中一個基本的事實是:CK為一有限
阿貝爾群,hK=|CK|稱為K的
類數。當hK=1,即每個理想都是主理想,OK為一
主理想環,從而因子分解唯一性定理成立。在一定意義上,理想類群CK與類數hK反映了代數數域K在
算術上的複雜性。直到現在,類群結構的研究與類數的計算,始終是代數
 公式9
公式9數論中重要問題之一。即使是
二次域類數的計算也是很困難的,一個值得注意的進展是
Heegner最先證明了(公式7)它們分別是d=1,2,3,7,11,19,43,67,163等9個被業界稱為Heegner 數。
正合列(2)的另一端是單位群UK,它的結構已被狄利克雷完全決定。他證明了UK=HK×VK,式中HK為K中全部
單位根組成的
有限群,VK是一秩為r1+r2-1的自由
阿貝爾群,r1為K 到
實數域R 同構的個數,2r2為K到
複數域C 同構(非實的)個數。VK的一組基稱為
基本單位組。具體算出基本單位組是代數
數論中又一個重要的問題。基本單位組與
類數有密切的聯繫。整數環中一個素數p 在OK中生成一個理想pOK,一般地,它不一定是OK中的素理想。研究素數p 在OK中的
素理想分解的規律,是代數數論中一個中心問題。下面把這個問題放在一個更廣的形式下來討論。
 公式10
公式10設L是代數
數域K上的一個l次擴張,L當然仍是一個代數數域。它的代數整數環為OL,顯然,(公式8)且OL為OK的一個有限生成模。
如果OL是OK上一自由模(秩一定是l),那么在OL中就有l個元素r1,r2,…,rl構成OL的一組基,即(公式9)這樣的元素組r1,r2,…,rl稱為OL對於OK的一組整基。當OK是
主理想環時,由主理想環上有限生成模的結構定理可知,OL對於OK一定有整基。特別地,代數
整數環OK對於整數環Z一定有整基。
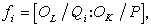 公式11
公式11設P是OK中一個
素理想。POL是OL中一個理想,它在OL中有素理想分解(公式10)
因為代數整數環是戴德金環,素理想都是極大理想,即代數整數環對於素理想的商環是域。對於(3),可以證明Qi∩OK =P,i=1,2,…,g。因而OK/P可以看作OL/Qi的
子域。令(公式11)它稱為Qi對於P的剩餘次數,ei稱為Qi對於P 的分歧指數。於是有(公式12)
 公式12
公式12如果在(3)中有某個ei>1,即POL被
素理想Qi的平方整除,就說P 在L 中分歧,而Qi就稱為在K上分歧。否則就稱為非分歧。如果OK中所有的素理想在L中都是非分歧的,L就稱為K 的一個非分歧擴張。
判別式與差積是刻畫分歧的兩個重要概念。令Tr表示有限擴張L到K 的跡。對於L中任意l個元素v1,v2,…,vl,可知det│Tr(vi,vj)│=0的
充分必要條件是v1,v2,…,vl,在K上
線性相關。在OL中取l個在K上
線性無關的元素v1,v2,…,vl,作(公式13)對於OL中所有可能的線性無關的元素組 v1,v2,…,vl,det│Tr(vi,vj)│在OK中生成一個理想Δ(L/K),它稱為L對於K的判別式。可以證明,OK中
素理想P在L中分歧,
若且唯若P|Δ(L/K)。由此可知,K中分歧的素理想只有有限多個,且L為非分歧擴張的
充分必要條件是:Δ(L/K)=OK。利用判別式可以證明,有理數域上沒有次數大於1的非分歧擴張。
 公式13
公式13 在L中定義C={v∈L│Tr(vOL)嶅OK},顯然C 是L的一個
分式理想,且C叾OL。令 δ(L/K)=C-1,它是OL中一個理想,稱為L對於K 的差積。可以證明,OL中素理想Q在K上分歧,若且唯若Q|δ(K/L)。差積與
判別式有密切聯繫。
 公式14
公式14研究代數數域的算術性質與代數性質之間的聯繫,是代數
數論的一個重要的方面。
設L/K是一伽羅瓦擴張,g=g(L/K)是伽羅瓦群。可以證明,在
分解式(3)中,
素理想Q1,Q2,…,Qg在伽羅瓦群 g下是可遷的,因而有即對於OK中素理想P有代數數論代數數論且Q1,Q2,…,Qg有相同的剩餘次數ƒ。公式(4) 就成為l=eƒg。 令 D1為 Q1在 g 中的穩定
子群,即代數數論代數數論,顯然【g:D1】=g,|D1|=eƒ。令 岧=OL/Q1,噖 =OK/P,於是D1中每個元素誘導出岧/噖 的一個自同構。可以證明,代數數論是一滿
同態。令K1為這個同態的核,顯然,【D1:K1】=ƒ,│K1│=e,D1稱為Q1的分解群,K1稱為Q1的惰性群。對Qi相應地有子群Di與Ki, 在g中它們分別與D1與K1共軛。當 P非分歧時,代數
數論代數數論(因噖、岧是
有限域)。由伽羅瓦基本定理,相應地有一串域代數數論代數數論是L的一個最大的域,P 在其中不分歧。當P 分歧時,群K1還可進一步細分,即定義所謂高階分歧群。這是由D.希爾伯特建立的一套重要的理論,稱為希爾伯特分歧理論。
對於代數數域上的阿貝爾擴張,有很深刻的結果,即所謂類域論。
唯一因子
代數數域K的
整數環OK的元素的素分解和整數環Z的素數分解有不同之處,不是每個OK的元素都唯一分解。雖然OK元素的唯一分解束在某些情況下可能成立,如高斯
整環,但在其它情況下可能會失敗, 如
二次域Z [√-5]中,6就不是唯一分解。
OK的理想類群是一個整數環OK的元素是否唯一因子分解的度量,特別是當整數環OK理想類群是平凡群時,
若且唯若O為
唯一分解整環OK元素的唯一分解可能成立:這時OK的理想的唯一分解成素理想(即它是一個戴德金整環)。這使得在研究OK的素理想尤其重要。從另方面,從
整數環Z更改為代數數域K的整數環OK後,整數環Z中素數就能生成Z素理想(其實,Z的每一個素理想(p)的形式是:pZ)可同一素數在O中可能不再生成素理想,例如,在高斯
整環中,理想2Z[i]不再是素理想,
但理想3Z[i]是一個素理想。高斯整環唯一因子分解完整的答案使用費爾馬大定理,其結果為:
得出這種簡單的結果對更一般的整數環來說是代數
數論的基本問題。當代數數域K是有理數Q的阿貝爾擴張時(即
阿貝爾群的伽羅瓦擴張)類域論實現了這一目標。
素元和素點
(根據類域論,因K為有理域Q時OK才有唯一分解,以下K=Q,注意有理域Q和有理數域不同,實域R和
實數域不同)
在OK
素理想的概念的一個重要的推廣是理想論,也叫
賦值論,這兩種方法之間的關係如下:
運算為通常的
絕對值函式|·|,映射有理域Q→實域R的,令絕對值函式|·|p: 定義稱為p-adic絕對
賦值,p∈Z中的素數。由
奧斯特洛夫斯基的定理,所有p-adic絕對賦值對Q是
等價類,p-adic絕對賦值可看成類似通常素數。更普遍的,代數數域K的絕對賦值稱為一個素點places。K中素元分兩類:像p-adic絕對賦值|·|p這種等價類是有限的,被稱為有限素元(有限素點)。而通過復域C的模|·|方式定義的素元可看成復域C一個無限子集,被稱為無限素元(或無限點)。因此,一般表示Q的素元集合為{2,3,5,7,...,∞},在這種情況下|·|∞是有理域Q的素元(素點)。
K的無限素元可有嵌入
同態K→C(即非零的環同態,從K到C)。具體來說,可把嵌入分成兩個不相交的
子集,那些像在R中算一個子集S1,其餘的為另一子集S2。S1的每個嵌入σ:K→R,對應唯一一個和通常絕對值一樣的絕對賦值;這種方式產生的一個素元的被稱為一個實素元(或實素點)。S2的一個嵌入τ:是K→C不包含在R中的的像,可以形成另一個唯一的嵌入τ,稱為
共軛嵌入,組成的復共軛映射為τ的C→C.而此絕對賦值為複數的模:|z| = |z| 。這樣的素元叫一個復素元(或復素點)。這樣無限素元的集合的描述如下:每個無限素元對應到一個唯一的。
 公式1
公式1 公式2
公式2 公式3
公式3 公式4
公式4 公式7
公式7 公式8
公式8 公式9
公式9 公式10
公式10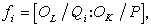 公式11
公式11 公式12
公式12 公式13
公式13 公式14
公式14
 公式1
公式1 公式2
公式2 公式3
公式3 公式4
公式4 公式7
公式7 公式8
公式8 公式9
公式9 公式10
公式10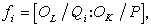 公式11
公式11 公式12
公式12 公式13
公式13 公式14
公式14