一個非零環R叫做一個整環(integral domain),整環是抽象代數中最基本的概念之一。對任意的a,b屬於環R,假如1、乘法適合交換律ab=ba;2、R有單位元e;3、R沒有零因子ab=0可得a=0或b=0,則R是整環。
基本介紹
- 中文名:整環
- 外文名:integral domain
- 概念:一個非零環R
- 運算:+和*
- 一級學科:數學
- 二級學科:抽象代數
定義
整環的商域



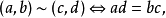













相關概念





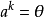








一個非零環R叫做一個整環(integral domain),整環是抽象代數中最基本的概念之一。對任意的a,b屬於環R,假如1、乘法適合交換律ab=ba;2、R有單位元e;3、R沒有零因子ab=0可得a=0或b=0,則R是整環。



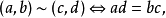


















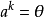







一個非零環R叫做一個整環(integral domain),整環是抽象代數中最基本的概念之一。對任意的a,b屬於環R,假如1、乘法適合交換律ab=ba;2、R有單位元e;3、R沒...
在抽象代數中,歐幾里得整環(Euclidean domain)是一種能作輾轉相除法的整環。凡歐幾里得整環必為主理想環。...
定義 準素整環(primary domain)平行於素環的概念.設R是交換環,若零理想是準素理想,則稱R為準素整環.換言之,R除冪零元外不含其他的零因子.整環是準素整...
歐氏環(Euclid ring)比主理想整環更窄的環類.它是整數環、域上一元多項式環有帶餘除法意義下的推廣。設R是整環,若存在R0=R-{ 0 }到非負整數集內的一個...
高斯整數環(ring of Gauss integers)是歐氏環的一個著名例子。設Z[i]={a+bi | a,b是整數,i為虛數單位}。 Z[i]對通常數的加法和乘法構成一個整環,稱為...
整表示是一類特殊的線性表示。設R是一個整環,其分式域為F,若群G在域F上的一個矩陣表示使得對任g∊G,矩陣T(g)的每個元素均在R中,則稱這種表示為整表示...
主理想環是在數學中使得每個理想均可由單個元素生成的環。若整環D的每一個理想都是主理想,則稱D為主理想環(principal ideal ring)。如果一個主理想環同時也是...
克魯爾環(Krull ring)以克魯爾命名的一類重要的整環,戴德金整環、一般的整閉諾特整環都是克魯爾環。...
歐氏環(Euclid ring)是比主理想整環更窄的環類。它是整數環、域上一元多項式環有帶餘除法意義下的推廣。設R是整環,若存在R°=R\{0}到非負整數集內的一...
素環是一類重要的環。若環R的零理想是素理想,則稱R為素環。整環、單環、本原環都是素環。素環與素理想有如下關係:P是R的素理想若且唯若R/P是素環。....
賦值環(valuation ring)是一種特殊的局部環。也是重要的交換環類。交換環R稱為賦值環。賦值環是交換的特殊序列。它與戴德金環有密切的關係。事實上,交換諾特局部...
在抽象代數中,分式環或分式域是包含一個整環的最小域,典型的例子是有理數域之於整數環。此外分式環也可以推廣到一般的交換環,此時通常稱作全分式環。 分式環有...
代數整數環(ring of algebraic integers)亦稱整數環,是一種特殊的交換整環,代數數域K中的代數整數全體OK稱為K的整數環,K是OK的商域,設L⊃K是兩個數域,則...
GCD環是一種有特殊性質的整環R,滿足其中任二個非零的元素都有最大公因數(GCD)。...... 唯一分解整環是GCD環,唯一分解整環是GCD環中恰好也是原子環(每一個非...
介紹 單一分解環(unique factorization ring)亦稱高斯環一種重要的整環類.設R是有單位元的整環,若R中任意元都能分解成有限個既約元的乘積,而且在相伴意義下...
2 唯一分解整環 3 公用工程流程圖 UFDUFD加密軟體 編輯 故障現象:隨身碟被分為兩個無法合併的分區,在設備管理中看到的是兩個物理驅動器,在沒有安裝UFD加密程式...
