基本介紹
- 中文名:主理想環
- 外文名:principal ideal ring
- 概況:整環D的每一個理想都是主理想
- 所屬學科:數理科學
- 例子:歐幾里德環、高斯整數環等
概念
定義
等價定義
相關性質定理
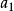
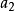
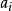
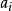
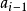
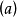
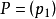
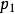
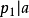
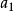
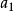
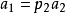
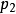

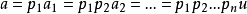

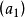
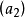
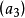
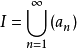
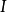
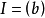
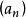
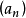
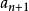
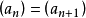
舉例分析
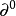
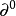

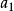
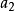
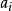
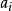
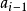
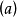
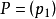
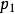
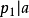
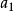
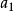
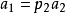
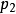

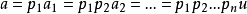

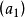
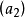
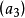
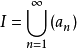
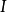
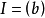
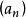
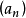
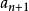
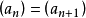
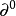
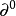
主理想環是在數學中使得每個理想均可由單個元素生成的環。若整環D的每一個理想都是主理想,則稱D為主理想環(principal ideal ring)。如果一個主理想環同時也是...
主理想整環是比單一分解環範圍更窄的整環類。若一個環R的任意理想都是主理想,則稱R為主理想環。若R同時又為整環,則R稱為主理想整環。整數環Z及域上一元...
理想類群(ideal class group)是數域的分式理想群按主理想子群分類所形成的群。數域K的兩個分式理想A和B稱為等價的,指存在α∈K使A=αB。K的分式理想等價類...
主理想定理(principal ideal theorem)希爾伯特類域的主要定理.該定理斷言:數域k的任一理想a到k的希爾伯特類域K上總為主理想,即aOK總為K的主理想,式中OK為K的...
歐氏環(Euclid ring)比主理想整環更窄的環類.它是整數環、域上一元多項式環有帶餘除法意義下的推廣。設R是整環,若存在R0=R-{ 0 }到非負整數集內的一個...
在抽象代數中,歐幾里得整環(Euclidean domain)是一種能作輾轉相除法的整環。凡歐幾里得整環必為主理想環。...
在交換環的情形,R的商環的自內射性與R上模的分解性有密切聯繫,即任意R模是循環模的直和若且唯若R是阿廷主理想環;若且唯若R是諾特環且對於任意理想I,R/I...
[3] 高斯整數環基本性質 編輯 (1)高斯整數環是歐幾里德整環。(2)高斯整數環是主理想整環。(3)高斯整數環是唯一因式分解整環R,滿足下列兩個條件:①...
這是因為在主理想環中,a和b的最大公約元被定義為理想aA + bA的生成元。裴蜀定理定理 編輯 在數論中,裴蜀定理是一個關於最大公約數(或最大公約式)的定理。...
本書在著重研究了主理想整環上的模及其分解後,來重新理解向量空間線上性運算元作用下的分解,使讀者從高-個層次上來認識線性代數。本書適合理工科專業的大學生、研究...
L的整閉包,OL也是有限生成的OK模,OK是戴德金環,其理想可惟一(不計次序)分解為其素理想的乘積,OK是惟一析因環若且唯若OK是主理想環,這也等價於K的理想類數...
