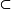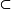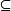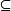理想(數學概念)

在序理論中，理想是偏序集合的一個特殊子集偏序，表示為集合(P,≤)的非空子集 I 稱為一個理想。在環論中，理想（Ideal）是一個抽象代數中的概念。理想的對偶概念，就是說通過反轉所有的 ≤ 並且交換V為A獲得的概念是濾子。

在整個數學學科中，理想的概念還涉及代數數論，是理想概念的推廣，也叫分式理想。

基本介紹

• 中文名：理想
• 外文名：Ideal
• 序理論：理想是偏序集合的一個特殊子集
• 環論：理想是一個抽象代數中的概念
• 相關領域：代數數論、數理邏輯
• 學科：數學

理想(ideal)（環論）

環R的一個非空子集I ，如果對於R的兩個代數運算，滿足條件：對任意a,b∈I,r∈R,有a-b∈I,ra∈I，則稱 I 是環R的一個左理想。類似有右理想定義。

環R的一個非空集合I，如果對於R的兩個代數運算，滿足條件：對任意a,b∈I,r∈R,有a-b∈I,ar∈I，則稱 I 是環R的一個右理想。

環R的一個非空子集I，如果既是左理想又是右理想，稱I為R的雙邊理想，通常簡稱I為R的理想。

理想 (序理論)

序理論中理想的最一般的定義如下：

偏序集合(P,≤)的非空子集 I 稱為一個理想，若 I 滿足：

1. I是下閉的。即，∀x ∈ I, y ∈ P, y ≤ x ⇒ y ∈ I。
2. I是有向的。即，∀x,y ∈ I，∃z ∈ I，使 x ≤ z，y ≤ z。

理想最初只在格上定義。與上述定義等價的定義如下： 格(P,≤)的非空子集 I 是理想，若且唯若：

1. I是下閉的。
2. I對於有限並(上確界)運算封閉，即，∀x,y ∈ I，有x ∨ y ∈ I。

理想（代數數論）

亦稱分式理想，是理想概念的推廣。設R為一整環，K為其商域（分式域），M K是R模。若存在非0的c∈R使cM={cm|m∈M} R，則稱M為分式理想。通常的理想（又稱整理想）也是分式理想。戴德金環的分式理想全體構成一個乘法阿貝爾群，由其素理想生成。

理想（集合論）

在集合論中，理想是一種特殊的集族。它與濾子相對偶。零S是一非空集，S上的理想F是由S的子集所組成的集族。它滿足下列條件：

1、 ，且 ；

2、若X∈F，且Y∈F，則X∪Y∈F；

3、若Y∈F，且X Y，則X∈F；

S上的理想F'被稱為素理想，如果對每個XS，有X∈F'或S-X∈F'。

理想概念是斯通（Stone，M.H.）於1934年提出的。