基本介紹
- 中文名:濾子
- 外文名:filter
- 屬性:一類集族
- 創始人:昂利·嘉當
- 引進時間:1937年
定義

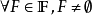
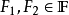
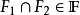

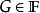


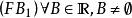
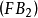
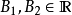


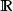
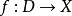

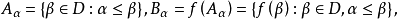

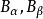



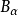





相關概念
定義1
定義2



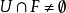




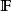
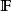
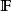
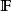
定義3
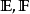
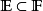




相關定理
定理1

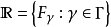



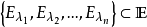


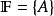
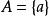
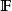



定理2
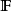
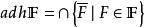
定理3


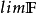
定理4

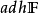

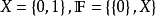

定理5

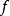

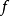
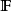
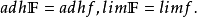
定理6



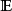
定理7
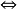


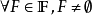
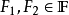
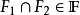

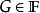


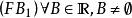
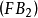
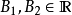


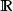
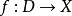

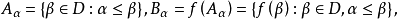

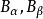



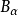








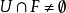




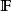
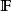
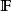
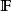
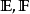
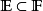





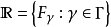



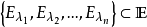


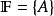
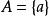
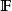



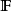
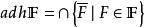


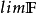

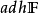

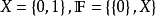


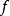

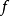
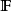
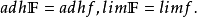



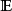
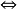
濾子是一類集族,設X是集合,F是X的非空子集族,若F滿足:1.F的任意兩個成員的交屬於F;2.若A∈F,A⊂B⊂X,且B∈F; 則稱F為X上的濾子。為了用極限...
極大濾子(maximal filter)亦稱超濾子,是一類特殊的濾子。設F是集合X上的濾子,若對於包含F的濾子H恆有F=H,則稱F為極大濾子,對於集合X上的任意濾子F,恆...
定義 濾子化環(filtered ring)一種與整數加群上的分次環有著密切聯繫的環一個有單位元1的結合環R,若存在R的加法子群升鏈{F R}nEZ},且滿足:1 E FoR, F...
α正則濾子(α-regular filter)一種具有正則性質的濾子.設a是一個基數,D是非空集I的一個真濾子,如果存在一個基數為a的集合EcD,能使對每個ZEI,僅有有限多...
α完全濾子(α-complete filter)一種保持少於α個元素的交的濾子.設α是一個無限基數,D是I上的一個濾子,如果D中任意少於α個元素的交仍屬於D(即若EcD,且}...
有界濾子(bounded filtration)一種特殊的濾子.設M={M‑{nEZ}是分次模,FM是M的一個濾子,若對每一個nEZ,有兩個整數u = u‑,v = vn,使得當p鎮u時...
定義介紹 濾子化模(filtered module)濾子化環在模中相平行的概念.設R是濾子化環,M為左R模.若存在M的子加群升鏈{F M}nEZ}使得 則稱M為濾子化模,子加...
完全濾子化模(complete filtered module)為濾子化模的特殊類,即M是濾子化左R模.M的元素的序列。...
介紹 伯恩施坦濾子(Bernstein filtration)一種標準的正濾子.在外爾代數A}<k)中,對整數v,0,用集合{x0aallal+iRl<}}(其中a-alaZ...a}}}/}-R}Rz w ...
可數不完全濾子(countably incomplete filter)不保持可數個元素的交的濾子.設D為非空集I上的濾子,如果存在一個可數子集EcD,能使門E諾D,則稱D為可數不完全...
鄰域濾子(neighborhood filter)一類特殊的濾子.拓撲空間X中點二的鄰域系是X上的濾子稱為二的鄰域濾子. ...
7. 關聯BCK 代數的P濾子、I 濾子及 BFI 濾子 《模糊系統與數學》 2005.9 第一 8. 泛邏輯學中 UB 代數系統的若干性質《計算機工程與套用》 2007.7 9...
首先回顧了Heyting代數的定義和有關性質,以及它與Boole代數的關係;其次,研究了Heyting代數中濾子的性質,給出了Heyting代數的濾子格的具體結構以及由子集生成的濾...
它蘊涵了序列、網和濾子的極限的唯一性。豪斯多夫得名於拓撲學的創立者之一費利克斯·豪斯多夫。豪斯多夫最初的拓撲空間定義把豪斯多夫條件包括為公理。...
