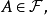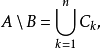集族是一種特殊的集合,以集合為元素的集合稱為集族。例如,集A的冪集P(A)是一個集族,P(P(A)),P(P(P(A))都是集族。又例如,由空集φ、集合A={1,2,3}作為元素的集合M={φ,A}是一個集族。 注意,由空集φ作為元素的集合是一個集族,它已不是空集,即A={φ},它不同於{ }。在這裡,A= {φ}是具有一個元素的集合,是單元素集。集族常用花體字母A,B,C等表示,取A為標號集,A到集族A的一一對應(雙射)為f:a→Aa,則集族A可記為{Aa|a∈A}或{Aa}a∈A。當A為線性序集{…,a,…,b,…,c,…}時,集族{…,Aa,…,Ab,…,Ac,…}稱為集列。
基本介紹
- 中文名:集族
- 外文名:family of sets
- 定義:以集合為元素的集合
- 常用集族:環、半環、代數、σ-代數等
定義




幾種常用集族
集族類別 | 等價定義 | 對運算的特性 |
半環 | 對交封閉,差為有限不相交並 | |
環 | 對“U”“\”封閉 對“U”“△”封閉 對“∩”“△”封閉 對“∩”,不相交並,包含差封閉 | 對一切有限 運算封閉 |
代數 | 含X的環 對“U” 余“ ' ’”封閉 對“∩” 余“ ' ’”封閉 | 含X且對一切有 限運算封閉 |
σ-代數 | 對  為代數且對遞增集序列並封閉 | 含X且對一切可 列運算封閉 |
半環





















環
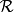
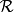














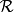

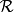
代數


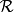
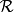



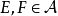





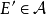
σ-代數