基本介紹
- 中文名:極大理想
- 外文名:maximal ideal
- 所屬學科:數學
- 相關概念:環、理想、素理想、素數等
定義

定理
定理1





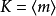









定理2

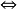





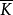



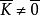


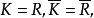














定理3

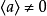

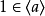

推論1




推論2










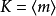










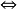





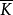



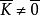


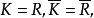















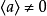

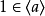








極大理想是一類特殊理想,設a是環R的左(右)理想,若a≠R且R中沒有真正包含a的左(右)理想,則稱a為R的一個極大左(右)理想。類似地,可定義極大理想,任意有...
極小理想是一類特殊理想,是與極大理想相對偶的概念。環R的一個左(右)理想a,若a不真含R的非零左(右)理想,則稱a為R的極小左(右)理想。類似地,可定義極...
極大濾子(maximal filter)亦稱超濾子,是一類特殊的濾子。設F是集合X上的濾子,若對於包含F的濾子H恆有F=H,則稱F為極大濾子,對於集合X上的任意濾子F,恆...
第一極大原理(first maximal principle)也稱佐恩引理,Zorn引理,是選擇公理的一個等價命題。該引理斷言:任給非空半序集,若其中每個全序子集(有時又稱為鏈)都有...
他關於極大理想的觀念,不僅革新了調和分析,而且對代數幾何的發展產生了很大影響.他建立的一般譜論,使得20世紀前30年中由D.希爾伯特(Hilbert)和馮·諾伊曼等建立的...
在數學中,局部環是只有一個極大理想的交換含麼環。局部環的概念由 Wolfgang Krull 於1938年引入,稱之為Stellenringe,英譯 local ring 源自扎里斯基。...
在P中引入一個偏序,定義為集合的包含關係,那么P中必然有一個極大元素,並且這個元素是R的真子集,從而R有一個極大理想。為了套用佐恩引理,需要證明P的任何一個...
在定義一般賦范環R後,蓋爾范特極富創造性地引進並抓住極大理想這一基本概念.他建立了R的特徵標空間到R的極大理想的空間之間的一一對應,定義了現稱為蓋爾范特...
此外, 它的一個較弱版本給出了仿射空間中的點與多項式環的極大理想之間的一一對應關係, 由此建立了代數和幾何之間的聯繫, 使得人們可以用交換代數的手段研究幾何問...
稱環A的理想 為素理想是說,剩餘環 為整環,這個條件等價於滿足下面的條件(1),(2)。(1)若 ,則或 或 ;(2) 。稱A的理想 為極大是說剩餘環 為域,這個...
它的重要性在於每一個群都能嵌入到某個代數閉群。若G是代數閉群,則F[G]是本原環且G的增廣理想ωF(G)是惟一極大理想。代數閉群群 編輯 群是一種只有一...
進一步的,布爾環的子集是環理想(素環理想,極大環理想),若且唯若它是相應的布爾代數的理想(素理想,極大理想)。布爾環模以環理想的商環對應於相應的布爾代數模...
這些概念符合布爾環A 中的素理想和極大理想的環理論概念。理想的對偶是濾子。布爾代數 A 的濾子是子集 p,對於在 p 中的所有 x,y 我們有 x <math>\land...
2.4素理想和極大理想 2.5環的同態、商域 2.6唯一分解整環 2.7主理想整環和歐氏環 *2.8高斯整數環與二平方和問題 2.9多項式環 2.10唯一分解整環上的多項式環...
3.dim R=1(其中dim表示克魯爾維數),也即R不是域且非零素理想均為極大理想.在戴德金整環R中每個準素理想均為素理想的冪,從而每個非零理想均可惟一(不計...
諾特模是抽象代數中一類滿足升鏈條件的模,定義方式類似諾特環。是一種重要的模。它是阿廷模的對偶概念。即滿足極大條件的模。若A模M的任一子模升鏈M1M2…都...
(主線為理想,講了素理想,極大理想,歐幾里得整環,主理想整環,因子分解整環等),域論(主線為域擴張,講了域擴張的途徑,域擴張的性質,域擴張的自同構群,伽羅瓦...
