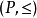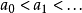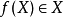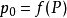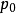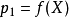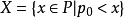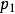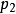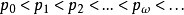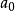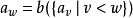第一極大原理(first maximal principle)也稱佐恩引理，Zorn引理，是選擇公理的一個等價命題。該引理斷言：任給非空半序集，若其中每個全序子集(有時又稱為鏈)都有上界，則該半序集有極大元，這條引理在近代數學中有廣泛套用，許多用選擇公理證明的命題，使用佐恩引理常常顯得更方便，例如，以下在代數、泛函、拓撲中出現的重要定理都是直接套用佐恩引理的結果：每個線性空間必存在基底；每個域的代數閉包存在且惟一；哈恩-巴拿赫擴張定理：任給線性空間的子空間上的線性泛函，必可擴張為全空間上的線性泛函；吉洪諾夫乘積定理：緊空間的拓撲乘積也是緊空間。佐恩引理首先作為定理被德國數學家豪斯多夫(F.Hausdorff)於1914年所證明，20年後，佐恩(M.Zorn)重新發現了它，證明了該命題與選擇公理等價(1935年)，此後，又利用它證明了任何集是可比較的，即任何集A，B，必有A≼B或B≼A(1944年)，稱之為“引理”，完全是由於歷史的沿襲。
基本介紹
- 中文名：第一極大原理
- 外文名：first maximal principle
- 別稱：佐恩引理，Zorn引理
- 所屬學科：數學（集合論）
- 簡介：選擇公理的一個等價命題
基本介紹,套用舉例,證明,
基本介紹
第一極大原理是集合論的一條重要引理，它由佐恩(M.A.Zorn)於1935年用選擇公理給以證明，該引理斷言：如果非空偏序集S的任何子鏈在S中有上界，則S至少有一個極大元素，佐恩引理與選擇公理等價，但它比選擇公理使用方便，它不僅是近世代數中的有力工具，而且已套用到其他許多數學分支中，通常人們也把由佐恩指出的另外4個與第一極大原理等價的命題稱為佐恩引理。它們是：
1.若偏序集S的任何良序子集均有上界，則S至少有一個極大元；
2.偏序集S必含有良序子集w，它沒有不屬於自己的上界；
3.圖基引理；
4.若C是一個關於映射的有限特徵條件，則在滿足C的映射中，有一個映射的定義域是極大元。
套用舉例
佐恩引理的一個典型套用是證明任何一個環R必然有極大理想。用P來表示R的所有真理想（即R的所有雙邊理想，且該理想是R的真子集）。在P中引入一個偏序，定義為集合的包含關係，那么P中必然有一個極大元素，並且這個元素是R的真子集，從而R有一個極大理想。
為了套用佐恩引理，需要證明P的任何一個全序子集T都有一個上界，即存在一個理想I滿足I is subset of R並且I比T中任何一個元素都大，但I並非R本身。現取I為T中所有理想的並。可以證明，I是一個理想：如果a和b是I中的兩個元素，那么必然存在T中兩個理想J, K ∈T滿足a ∈J, b ∈K。注意T是一個全序集，所以必然有J is subset of K或者K is subset of J，從而必然有a, b ∈J或a, b ∈I二者居其一，從而a + b ∈I。進一步，對於任何r ∈R, a ∈I都可以證明ra ∈I。由此，I成為R的一個理想。
現在考慮證明的核心部分：利用I = R充要於1 ∈I，可以證明I一定是R的真子集。因為如果1 ∈I，那么必然有某個J ∈T滿足1 ∈J，這意味著J = R，這與T的選取是矛盾的。
這樣，利用佐恩引理，P必然包含一個最大元素，而這個元素就是R的一個極大理想。
注意這個結論只在R是單位環的時候成立，在R不是單位環的情形下，一般而言這個結論是不成立的。
證明
從選擇公理證明佐恩引理的思路：
假設佐恩引理不成立，那么存在一個非空的偏序集
，使得它的任何一個全序子集都有上界，但P中任何元素都不是極大元素。然後，對於任何一個全序子集T，可以定義一個相對應的元素b(T)，使其嚴格大於T的任意元素，因為T有一個上界，P中又必然存在一個元素嚴格大於這個上界。為了確實地定義函式b，我們需要用到選擇公理。
利用函式b，可以構造 P的一個全序子集
，這裡作為下標的指標集不僅可以是自然數，也可以是序數。事實上，所有序數組成一個真類，粗略地說，可以認為序數的數目大於任何集合的基數，P也不例外。所以這個序列終會窮盡，這樣就導出了矛盾。
事實上這個證明的結論略強於佐恩引理：
我們也可以直接套用選擇公理證明佐恩引理：
根據選擇公理，對於一個偏序集P的所有非空子集X在存在一個選擇函式 f使得
。從 P本身開始：考慮
，如果
是極大元素則終止，否則構造
，這裡
，如果
是極大元素則終止，否則用相同的技術構造
。
於是我們獲得了P一個全序子集：
根據假設上述全序子集是有上界的。如果上界是上述全序子集中的元素則終止，否則繼續上述步驟，最終總能夠窮盡P。
不過需要說明的是上述證明並沒有闡明為何最終能夠窮盡P，是一個不夠嚴格的證明。見於 Lectures on the Hyperreals -- An Introduction to Nonstandard Analysis 一書。
