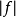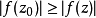最大模原理

在複分析中，最大模原理說明如果單變數複變函數 f 是一個全純函式，那么它的模|f| 的局部最大值不可能在其定義域的內部取到。

基本介紹

• 中文名：最大模原理
• 外文名：maximum modulus principle
• 原理：不恆為常數的函式達不到最大值
• 例外：常數函式
• 套用學科：數學
• 套用領域：複分析

定義

在複分析中，最大模原理說明如果單變數複變函數f是一個全純函式，那么它的模的局部最大值不可能在其定義域的內部取到。

換句話來說，全純函式f要么是常數函式，要么對於任意的在其定義域之內的z₀，都存在一個足夠靠近它的點z，使得f在後者上的取值的模 |f(z)| 比 |f(z)₀| 更大。

正規定義

設f為在複平面C的某個連通開子集D上定義的單復變全純函式。如果z₀是D中一點，使得對它任意鄰域上的其它的點z都有，那么函式f是在D上的常數函式。

證明概要

首先注意到等式：

• logf(z) = log |f(z)| + i argf(z)
  

於是，對於復變數自然對數， log |f(z)| 是一個調和函式。 由於z₀是這個函式的一個局部極大值，根據極大值定理，|f(z)| 在定義域上是常數。因此，運用柯西-黎曼方程可以得到：f'(z)=0。於是可以推出f(z) 是一個常數函式。

通過取倒數，可以得到對應的最小模原理。後者聲稱如果f在一個有界區域D內是全純函式，並在其邊界上連續，且在所有點上非零，那么函式 |f(z)| 的最小值只會在D的邊界上取到。

同時，最大模原理可以被看作是所謂的開映射定理的一個特例。開映射定理聲稱，一個全純函式必然將開集映射到開集。如果 |f| 在定義域內部一點a達到極大值，那么a的一個足夠小的領域在f映射下的像集必然不是開集。於是，f必然是常數函式。

套用

最大模原理在複分析的許多領域中都有著套用，可以產生很多重要的結果，比如：

• 用於證明代數基本定理：使用最大模原理的證明是一個基本的複分析的證明，可以在很多複分析教材中看到。
  
• 用於證明施瓦茨引理，一個在複分析中有廣泛引套用並可以推出很多結果的定理。
  
• 其推廣是弗拉格門-林德洛夫原理，將結果擴展到定義域無界的函式。