劉維爾(Liouville)定理是複變函數中的基本定理之一,其內容可簡單描述為“一個有界的整函式必是常函式"。
註:整函式為在有限複平面上解析的複函數。
基本介紹
- 中文名:劉維爾定理
- 外文名:Liouville's theorem
- 提出者:劉維爾(Joseph Liouville)
- 套用學科:複變函數
- 適用領域範圍:
定理內容
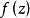
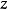
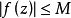
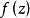
定理證明
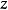
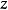

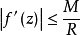
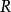
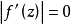
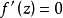
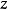
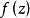
重要推論
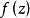
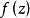
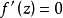
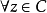
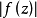
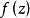
套用
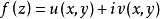
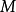
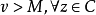
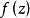
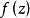
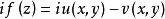
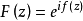
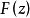
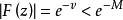
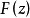
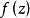
劉維爾(Liouville)定理是複變函數中的基本定理之一,其內容可簡單描述為“一個有界的整函式必是常函式"。
註:整函式為在有限複平面上解析的複函數。
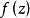
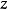
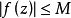
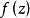
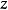
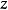

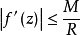
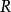
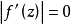
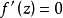
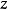
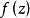
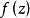
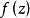
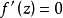
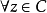
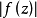
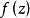
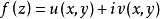
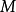
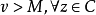
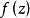
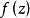
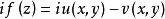
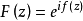
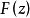
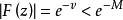
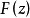
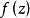
劉維爾(Liouville)定理是複變函數中的基本定理之一,其內容可簡單描述為“一個有界的整函式必是常函式"。注:整函式為在有限複平面上解析的複函數。...
在量子力學的海森堡繪景里,埃倫費斯特定理非常顯而易見;取海森堡方程的期望值,就可以得到埃倫費斯特定理。埃倫費斯特定理與哈密頓力學的劉維爾定理密切相關;劉維爾定理...
皮卡小定理說明,如果函式 是整函式且不是常數,則 的值域或者是整個複平面,或者只去掉一個點。 這個定理在1879年證明。它強化了劉維爾定理:任何不是常數的整函式...
利用劉維爾定理(有界的整函式一定是常數),可知1/p是常數,因此p是常數。於是得出矛盾,所以p(z0) = 0。證明三這個證明用到了輻角原理。設R為足夠大的正實數,...
伯克霍夫遍歷定理(Birkhoff ergodic theorem)是遍歷論的第一個重要結果。遍歷理論...吉布斯建立了完整的統計系綜方法,類比於流體力學中的劉維爾定理,證明了系綜的...
當∞點是整函式的可去奇點時,這個整函式只能是常數,這就是著名的劉維爾定理,通常表述為“有界整函式必為常數”。整函式劉維爾定理 編輯 ...
劉維爾定理與 Roth 定理劉維爾定理可用以直接構造超越數。在這之前,數學家們已藉連分數導出關於平方根與其它二次無理數的許多逼近性質。這個結果後來由 Axel Thue...
根據劉維爾定理每個辛同胚保持相空間的體積形式不變。由哈密頓流導出的辛同胚的族通常稱為哈密頓系統的哈密頓力學。哈密頓矢量場也導出一個特殊的操作,泊松括弧。...
若無劉維爾定理,我們可以摹想相空間中區域的毫無疑義的發散趨勢可由整個空間的縮小而補償。然而,這一個定律告訴我們這是不可能的,而我們必須面對這個驚人的含義—...
如果f在整個R都有定義的調和函式,並且在其上有最大值或最小值,那么函式f是常數函式(參見複平面上函式的劉維爾定理)。調和函式推廣 編輯 調和函式研究的一個推廣...
根據劉維爾定理每個辛同胚保持相空間的體積形式不變。由哈密頓流到處的辛同胚的族通常稱為哈密頓系統的哈密頓力學。哈密頓矢量場也導出一個特殊的操作,泊松括弧。...
根據劉維爾定理每個辛同胚保持相空間的體積形式不變。由哈密頓流到處的辛同胚的族通常稱為哈密頓系統的哈密頓力學。哈密頓向量場也導出一個特殊的操作,泊松括弧。...
2.1.5 泊松定理2.2 正則變換2.2.1 母函式的正則方程2.2.2 泊松括弧的不變性2.2.3 無窮小相切變換2.3 劉維爾定理2.3.1 劉維爾定理證明2.3.2 維里...
來表示,因而由(3)得到由此利用解析開拓和廣義劉維爾定理求出φ()和()(準確到相差一個整函式),然後再對φ()進行傅立葉逆變換即可求得方程(1)的解()。...
比較構造性證明與傳統證明,可以看出,雖然布勞威的證明確實是比使用劉維爾定理的證明更長,但構造性證明比傳統證明給出的“信息量”要多得多。比如布勞威的方法能求出...
的劉維爾定理,證明了系綜的機率分布守恆定理。如果用φt(P)表示相點P 經過時間t之後在相空間中達到的點,那么φt便是相空間的一個變換。所謂機率守恆,就是說...
複變函數論中的劉維爾定理告訴人們:平面上的有界全純函式只能是常值函式。常值函式是周期函式,但沒有最小正周期常函式定義和性質 1、周期函式的定義:對於函式y...
正則變換是哈密頓-亞可比方程與劉維爾定理的基礎。 [1] 中文名 正則變換 外文名 canonical transformation 套用學科 力學 適用領域範圍 天體力學 實質 保持正則...
因為辛同胚保持辛 2-形式,從而也保持辛體積,於是有哈密頓力學中的劉維爾定理。由哈密頓向量場生成的辛同胚也成為哈密頓辛同胚。因為{H,H} =XH(H) = 0,哈密...
哈密頓向量場定義了辛流形上的一個流場,稱為哈密頓流場或者叫辛同胚。根據劉維爾定理,哈密頓流保持相空間的體積形式不變。中文名 辛流形 外文名 Symplectic ...
另一個重要結果是劉維爾定理,它斷言定義在整個 上的有界調和函式必為常數函式。除此之外,還有柯西估計、Harnack 不等式與施瓦茨引理等幾個重要的不等式。...
正則變換§46 劉維爾定理§47 哈密頓一雅可比方程§48 分離變數§49 絕熱不變數§50 正則變數§51 絕熱不變數守恆精確性§52 條件周期運動朗道撰寫的第一版序...
會得到一個主方程,是林德布勞德方程的特例,而林德布勞德方程可視為劉維爾定理的量子力學版本。 [1] 耗散系統相關條目 編輯 遊蕩集 非平衡態熱力學 非平衡態熱力...
當∞點是整函式的可去奇點時,這個整函式只能是常數,這就是著名的劉維爾定理,通常表述為“有界整函式必為常數”。參考資料 1. 《數學辭海》總編輯委員會.《...
