基本介紹
- 中文名:調和函式
- 外文名:Harmonic function
- 滿足:拉普拉斯方程
- 屬於:函式
- 領域:數學
- 套用學科:數學
- 相關術語:複變函數
定義


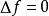
例子
- 函式:f(x1,x2) =exp(x1)sin(x2)。
- n元的調和函式的例子有:
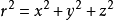
| 函式 | 奇點 |
|---|---|
 | 原點處的點電荷 |
 | 原點處的x-向電偶極矩 |
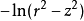 | 整個z-軸上均勻帶電的線電荷 |
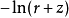 | 負的z-軸上均勻帶電的線電荷 |
 | 整個z-軸上的線性電偶極矩 |
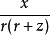 | 負的z-軸上的線性電偶極矩 |
性質
聯繫
規則性的理論
極大值定理
介值性質
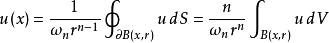




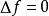
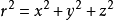
| 函式 | 奇點 |
|---|---|
 | 原點處的點電荷 |
 | 原點處的x-向電偶極矩 |
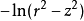 | 整個z-軸上均勻帶電的線電荷 |
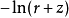 | 負的z-軸上均勻帶電的線電荷 |
 | 整個z-軸上的線性電偶極矩 |
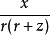 | 負的z-軸上的線性電偶極矩 |
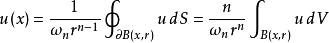

調和函式是在某區域中滿足拉普拉斯方程的函式。通常對函式本身還附加一些光滑性條件,例如有連續的一階和二階偏導數。當自變數為n個(從而區域是n維的)時,則稱它為...
下調和函式(subharmonic function)亦稱次調和函式,是亞調和函式的一個子類。若-f為上調和函式,則f稱為同一區域內的下調和函式,此時,若φ(t)是t的單調增的凸...
帶調和函式(zonal harmonic function)一類具有特殊性質的球面調和函式.由等式 確定的k次球面調和函式Z歲t')稱為以x'為極點的k次帶調和函式,其中交飛為k次球面...
在Brelot調和空間(X,H)中,設G為開集,則稱H(G)中的函式為G上的調和函式。對G上的下半連續函式u,若G中每一點x有一個開鄰域Vx,使得對任何一個閉包包含於...
立體調和函式(solid harmonics)拉普拉斯方程在直角坐標系下的n次齊次函式解.對於正整數n,存在2n+1個線性無關的n次立體調和函式.在球坐標系中寫出,即為r0Y,. (...
調和函式極值原理(extremism principle for harmonic function)調和函式的重要性質.在區域 D內調和且不恆等於常數的函式u(z),在D的內點不能達到最大值和最小值....
球面調和函式(spherical harmonic function)又稱球函式,是調和函式的一種。...... 當n級球體調和函式用球極坐標:γ(矢徑的大小),θ(余緯度),ψ(經度)表示為A(...
面調和函式(surface harmonics)有時亦稱球函式.即拉普拉斯方程齊次多項式解的角向部分.將拉普拉斯方程在球坐標系((r, B,卯下的解寫成r'Y (B,卯的形式((n為正...
球調和函式(spherical harmonics function )球體調和函式與球面調和函式的總稱.R”上的k次齊次調和多項式稱為k次球體調和函式,它在單位球面上的限制稱為k次球面調和...
不變調和函式,是拉普拉斯一貝爾特拉米方程。...... 不變調和函式,是拉普拉斯一貝爾特拉米方程。不變調和函式(invariant harmonic function)拉普拉斯一貝爾特拉米方程。u=。...
“圓柱調和函式”是天文學專有名詞。來自中國天文學名詞審定委員會審定發布的天文學專有名詞中文譯名,詞條譯名和中英文解釋數據著作權由天文學名詞委所有。...
在數學中,多重調和函式(Multiple harmonic function)將成為複雜分析中使用的一類重要的函式。 通常縮寫為psh,plsh。 在科勒流形上,多個諧波函式構成了諧波函式的一...
《調和函式理論》是2004年世界圖書出版公司出版的圖書,作者Paul Bourdon。...... 《調和函式理論》是2004年世界圖書出版公司出版的圖書,作者Paul Bourdon。...
橢球調和函式(ellipsoidal harmonics)是拉普拉斯方程的一種特殊形式的多項式解。對於給定的非負整數n,獨立的n次橢球調和函式有2n+1個:n為偶數時為(n/2)+1個第...
在數學中,重調和方程是在連續力學領域產生的四階偏微分方程,包括線性彈性理論和斯托克斯流的解。最簡單的高階橢圓型偏微分方程.方程▽ku=0(▽為拉普拉斯運算元,k為...
極小調和函式(minimal harmonic function)不計一個正的常數因子時比別的同類函式都小的非負非零調和函式.設口為拓撲空間,一族由口到[0,+二)的連續函式u組成的...
調和延拓(harmonic continuation),是位勢論中的一個概念,是指把調和函式的定義域擴大的過程或所得的函式。...
球體調和函式(spheroidal harmonic function)是調和函式的一種,即以變數x,y,z的齊次多項式表示的調和函式。以n次齊次多項式表示的調和函式稱為n級球體調和函式;當n...
貝塞爾函式是貝塞爾方程的解,它們和其他函式組合成柱調和函式。除初等函式外,在物理和工程中貝塞爾函式是最常用的函式,它們以19世紀德國天文學家F.W.貝塞爾的姓氏...
調和級數(英語:Harmonic series)是一個發散的無窮級數。調和級數是由調和數列各元素相加所得的和。中世紀後期的數學家Oresme證明了所有調和級數都是發散於無窮的。...
調和不變性(invariance of harmonicity)描述調和函式在某種變換之下的像保持調和的一個概念.所謂調和不變性,是指Rz的調和性在共形映射下不變,即區域DCRz內調和的...
過分函式(excessive function)是現代馬爾可夫過程理論的重要概念。過分函式與古典位勢理論中的上調和函式有著十分密切的聯繫,在布朗運動過程情形下,非負上調和函式就是...
調和映射(harmonic map)黎曼流形之間的一類十分重要的可微映射。數學上,在黎曼流形M和N之間的一個(光滑)映射,稱為調和映射。...
哈納克定理是關於單調遞增調和函式序列的收斂定理,由德國數學家哈納克提出。...... 哈納克定理是關於單調遞增調和函式序列的收斂定理,由德國數學家哈納克提出。...
