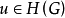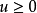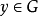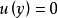基本介紹
- 中文名:局部超調和函式
- 外文名:locally hyperharmonic function
- 特點:每一點的某個鄰域上有超調和性
- 所屬學科:位勢論(公理化位勢論)
基本介紹,相關定理,
基本介紹
局部超調和函式(locally hyperharmonic function)是指在每一點的某個鄰域上有超調和性的函式。設U是一個開集,u是U上的取值於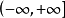 的下半連續函式,如果對每一
的下半連續函式,如果對每一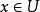 ,存在
,存在 的開鄰域
的開鄰域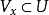 ,使得對任何滿足
,使得對任何滿足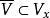 的正則區域
的正則區域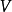 ,在
,在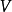 上恆有
上恆有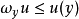 (
(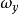 是V的U調和測度),那么u稱為U上的(相對於H的)局部超調和函式,記
是V的U調和測度),那么u稱為U上的(相對於H的)局部超調和函式,記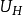 為U上的局部超調和函式全體,則
為U上的局部超調和函式全體,則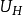 是X上的超調和簇,稱為由H產生的超調和簇,並且,H就是與
是X上的超調和簇,稱為由H產生的超調和簇,並且,H就是與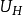 相關的調和簇。
相關的調和簇。
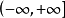
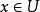

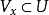
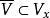
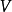
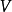
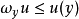
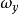
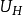
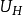
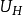
相關定理
證明: 設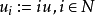 ,則
,則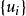 為
為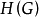 中的單調增加列,因為
中的單調增加列,因為 有界(實際上,每個
有界(實際上,每個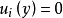 ),由公理3知
),由公理3知
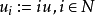
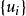
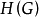

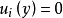
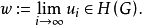
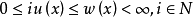
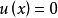
引理2 設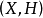 是Brelot調和空間,D是一個正則區域,W是一個開集使得
是Brelot調和空間,D是一個正則區域,W是一個開集使得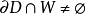 .那么對D中每個x成立
.那么對D中每個x成立
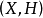
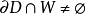
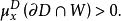
引理3 設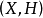 是Brelot調和空間,D是X的一個區域,
是Brelot調和空間,D是X的一個區域,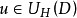 。若u在D的一個非空開子集W上恆等於
。若u在D的一個非空開子集W上恆等於 ,則它在D上也恆等於
,則它在D上也恆等於 .換言之,u在D要么恆等於
.換言之,u在D要么恆等於 ,要么在D的一個稠密子集恆等於
,要么在D的一個稠密子集恆等於 。
。
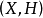
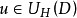




證明:設 {
{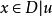 在x的一個開鄰域上恆等於
在x的一個開鄰域上恆等於 },顯然A是包含W的開集,我們斷言A=D,否則,設G是A的一個連通分支,於是
},顯然A是包含W的開集,我們斷言A=D,否則,設G是A的一個連通分支,於是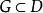 且
且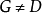 .因D是連通的,
.因D是連通的, 非空,設
非空,設 .因
.因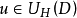 ,由局部超調和函式的定義,存在z的一個開鄰域V,使得對任何一個閉包包含在V的正則區域U都有
,由局部超調和函式的定義,存在z的一個開鄰域V,使得對任何一個閉包包含在V的正則區域U都有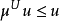 ,取定一個
,取定一個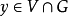 及一個正則區域U使得
及一個正則區域U使得 且U的閉包包含在
且U的閉包包含在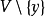 .因為G是連通的,故
.因為G是連通的,故 非空。由於u在
非空。由於u在 上恆等於
上恆等於 ,據上一引理知:對任意
,據上一引理知:對任意 有
有 ;故
;故

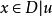

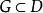
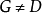


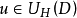
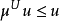
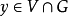

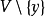






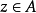
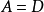
定理4 設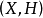 是Brelot調和空間,D是X的一個區域,
是Brelot調和空間,D是X的一個區域,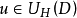 且在D上有
且在D上有 ,若存在D中的點z使得
,若存在D中的點z使得 ,則
,則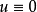 。
。
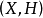
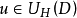


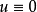
證明:令 ,則G為開集,若G非空,令
,則G為開集,若G非空,令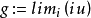 ,顯然,
,顯然,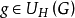 .因為在G上
.因為在G上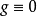 。由上一引理知,在D上也有
。由上一引理知,在D上也有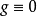 ,這表明對任意
,這表明對任意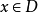 有
有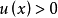 。
。

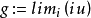
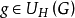
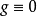
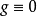
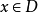
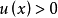
定理5 設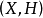 是Brelot調和空間,G是開集,若存在
是Brelot調和空間,G是開集,若存在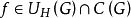 使得
使得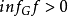 ,則G是相對於
,則G是相對於 的一個MP集。
的一個MP集。
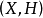
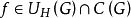
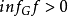

定理6 若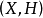 是Brelot調和空間,則
是Brelot調和空間,則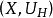 是一個
是一個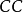 調和空間,而且每個局部超調和函式都是超調和函式,即:若G是開集,
調和空間,而且每個局部超調和函式都是超調和函式,即:若G是開集,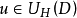 ,則在任何一個其閉包包含於G的正則區域D上有
,則在任何一個其閉包包含於G的正則區域D上有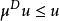 。
。
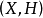
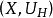
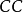
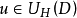
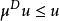
(關於文中所有結論的詳細證明請參考相應書籍)。