定義 設u(z)為區域 D 內的實連續函式，Z。是 D 內的任意一點，存在鄰域B（Z。，δ） ，當0<r<δ 時成立不等式
，則稱u(z)為區域D內的次調和函式（或稱下調和函式）.
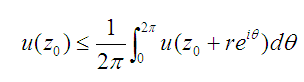
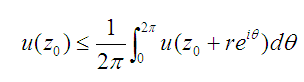
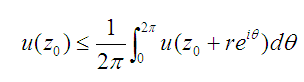
在數學中,多重調和函式(有時縮寫為psh,plsh或plush函式)形成複雜分析中使用的一類重要函式。 在卡勒廖流形上,多重調和函式形成了次調和函式的一個子集。 然而,...
定義 設u(z)為區域 D 內的實連續函式,Z。是 D 內的任意一點,存在鄰域B(Z。,δ) ,當0<r<δ 時成立不等式 ,則稱u(z)為區域D內的次調和函式(或稱...
調和函式是在某區域中滿足拉普拉斯方程的函式。通常對函式本身還附加一些光滑性條件,例如有連續的一階和二階偏導數。當自變數為n個(從而區域是n維的)時,則稱它為...
下調和函式(subharmonic function)亦稱次調和函式,是亞調和函式的一個子類。若-f為上調和函式,則f稱為同一區域內的下調和函式,此時,若φ(t)是t的單調增的凸...
過分函式(excessive function)是現代馬爾可夫過程理論的重要概念。過分函式與古典位勢理論中的上調和函式有著十分密切的聯繫,在布朗運動過程情形下,非負上調和函式就是...
橢球調和函式(ellipsoidal harmonics)是拉普拉斯方程的一種特殊形式的多項式解。對於給定的非負整數n,獨立的n次橢球調和函式有2n+1個:n為偶數時為(n/2)+1個第...
球函式(spherical function)通常指連帶勒讓德方程的解,亦即連帶勒讓德函式。有時也把面調和函式稱為球函式。在球坐標系中用分離變數法解拉普拉斯方程或亥姆霍茲方程...
球調和函式(spherical harmonics function )球體調和函式與球面調和函式的總稱.R”上的k次齊次調和多項式稱為k次球體調和函式,它在單位球面上的限制稱為k次球面調和...
立體調和函式(solid harmonics)拉普拉斯方程在直角坐標系下的n次齊次函式解.對於正整數n,存在2n+1個線性無關的n次立體調和函式.在球坐標系中寫出,即為r0Y,. (...
數學中研究多個復變數的全純函式的性質和結構的分支學科,有時也稱多複分析。它...定義:具有窮竭的多重次調和函式的域稱為擬凸域。根據Cartan Thullen定理,不難...
多重次調和函式(185) 39. 偽凸域(191)14. 全純包40. 單葉包(197) 41. 多葉包(202) 42. 奇點集的解析性(207)問題第iv章 亞純函式和留數...
《複變函數論》從套用的角度出發,從現代數學的觀點介紹複分析的基礎知識與常用工具,還包括格林函式,貝格曼核,次調和函式等內容。《複變函數論》敘述清楚、精闢簡要...
是構造全純函式的重要工具,而這在以往的教材中是不被重視的.又如,在介紹調和函式理論(第8章)的同時,我們還介紹了次調和函式的基本理論,因為次調和函式的理論在...
位勢論是數學的一支,它可以定義為調和函式的研究。“位勢論”一詞的來源在於,在19世紀的物理學中,自然界的基本力被相信為從滿足拉普拉斯方程的位勢導出。因此,...
首先要把擬凸域的概念拓廣,使之包括邊界不光滑的域可以給出與邊界的光滑性無關的擬凸域的概念.設Ω是Cⁿ中的域,如果在Ω上存在連續的多重次調和窮竭函式,...
基本概念如全純域、多次調和函式等;經典問題如Levi問題,Cousin I、II問題(單復變Weierstrass, Mittag-Leffler相應問題的推廣)等;與代數、幾何、分析緊密相關的重要...
38.多重次調和函式39.偽凸域14.全純包40.單葉包41.多葉包42.奇點集的解析性問題第Ⅳ章亞純函式和留數15.亞純函式43.亞純函式的概念...
多重次調和函式(185) 39. 偽凸域(191)14. 全純包40. 單葉包(197) 41. 多葉包(202) 42. 奇點集的解析性(207)問題第iv章 亞純函式和留數...