在數學中,多重調和函式(有時縮寫為psh,plsh或plush函式)形成複雜分析中使用的一類重要函式。 在卡勒廖流形上,多重調和函式形成了次調和函式的一個子集。 然而,與次調和函式(其在黎曼流形上定義)不同,多重調和函式可以在複雜的分析空間中完全一般地定義。
基本介紹
- 中文名:多重次調和函式
- 外文名:Plurisubharmonic function
- 領域:數學
- 英文縮寫:psh
- 地位:複雜分析中使用的一類重要函式
- 相關名詞:調和函式
簡介
正式定義


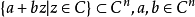


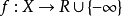

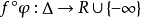

可微分的次調和函式


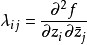
歷史
屬性


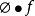



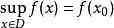

在數學中,多重調和函式(有時縮寫為psh,plsh或plush函式)形成複雜分析中使用的一類重要函式。 在卡勒廖流形上,多重調和函式形成了次調和函式的一個子集。 然而,與次調和函式(其在黎曼流形上定義)不同,多重調和函式可以在複雜的分析空間中完全一般地定義。


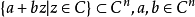


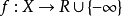

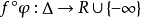



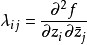


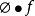



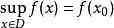

在數學中,多重調和函式(有時縮寫為psh,plsh或plush函式)形成複雜分析中使用的一類重要函式。 在卡勒廖流形上,多重調和函式形成了次調和函式的一個子集。 然而,...
在數學中,多重調和函式(Multiple harmonic function)將成為複雜分析中使用的一類重要的函式。 通常縮寫為psh,plsh。 在科勒流形上,多個諧波函式構成了諧波函式的一...
多重次調和窮竭函式(plurisubharmonic ex-haustive function)多復變函式論中一類重要的實函式...
數學中研究多個復變數的全純函式的性質和結構的分支學科,有時也稱多複分析。它...定義:具有窮竭的多重次調和函式的域稱為擬凸域。根據Cartan Thullen定理,不難...
多重次調和函式(185) 39. 偽凸域(191)14. 全純包40. 單葉包(197) 41. 多葉包(202) 42. 奇點集的解析性(207)問題第iv章 亞純函式和留數...
若將定義中的次調和函式改為多重次調和函式,得到的集合稱作多重極性集。極性集性質 編輯 中的單點集合是極性的 可數個極性集的聯集也是極性的 極性集的...
38.多重次調和函式39.偽凸域14.全純包40.單葉包41.多葉包42.奇點集的解析性問題第Ⅳ章亞純函式和留數15.亞純函式43.亞純函式的概念...
多重次調和函式(185) 39. 偽凸域(191)14. 全純包40. 單葉包(197) 41. 多葉包(202) 42. 奇點集的解析性(207)問題第iv章 亞純函式和留數...
全書共8章,全純函式與全純映照、延拓定理、復解析集,全純域、次調和函式與多重次調和函式、e運算元的存在性定理和L2方法等。[1] ...
