定義 設u(z)為區域 D 內的實連續函式，Z。是 D 內的任意一點，存在鄰域B（Z。，δ） ，當0＜r＜δ 時成立不等式，則稱u(z)為區域D內的次調和函式（或稱下調和函式）.
基本介紹
- 中文名：次調和函式
- 所屬學科：數學
次調和函式
次調和函式
相關詞條
- 次調和函式
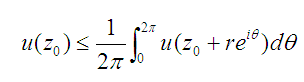
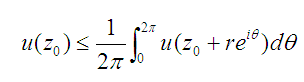
定義 設u(z)為區域 D 內的實連續函式，Z。是 D 內的任意一點，存在鄰域B（Z。，δ） ，當0＜r＜δ 時成立不等式，則稱u(z)為區域D內的次調和函式（或稱下調和函式）....
- 下調和函式
下調和函式(subharmonic function)亦稱次調和函式，是亞調和函式的一個子類。若-f為上調和函式，則f稱為同一區域內的下調和函式，此時，若φ(t)是t的單調增的凸函式，則φ°f為下調和函式。例如，當u(x)為D⊂R²上的復值解析函式，實數α>0時，|u(x)|與αlog|u(x)|都是下調和函式。定義 定義一：...
- 調和函式
調和函式滿足以下的極大值定理：如果K是U的一個緊子集，那么f在K上誘導的函式只能在邊界上達到其最大值和最小值。如果U是連通的，那么這個定理意味著f不能達到最大值和最小值，除非它是常數函式。對於次調和函式也有同樣的定理。介值性質 設B(x,r)是一個以x為中心，以r為半徑的完全在U中的球，那么調和...
- 多重次調和函式
是下面集合中的次調和函式：完全一般性，這個概念可以在任意的複雜流形或甚至複雜的分析空間X上定義如下。一個上半連續函式 被叫做次調和若且唯若對於任何全息圖 ，下面函式是次調和的：其中 表示單位圓。可微分的次調和函式 如果f是 類，那么若且唯若隱式矩陣 ，f被稱為Levi矩陣，且 是正半定數。歷史 ...
- 半空間中次調和函式的Matseav 定理
《半空間中次調和函式的Matseav 定理》是依託北京工商大學，由張艷慧擔任項目負責人的青年科學基金項目。項目摘要 近年來研究函式的增長性質成為位勢論中一個熱門的新方向。 許多物理問題都需要考慮函式的增長性，它是數學理論基礎同物理問題相結合的必然發展。 本項目基於單復變中經典的Matseav定理，擬研究高維空間中...
- 多重調和函式
是一個單調遞減的多重諧波函式系列， 也是一個單調遞減的多次諧波函式。所有連續的多次諧波函式可以作為單調遞減的一系列平滑多次諧波函式的極限得到。此外，這一行可以被選為統一收斂序列。正態半連續的不等式條件保持為方程。也就是說， 是多排諧波，以下為成立。多重次調和函式是可選的科勒稱重對分諧波方式是。因...
- 多重次調和窮竭函式
多重次調和窮竭函式(plurisubharmonic ex-haustive function)多複變函數論中一類重要的實函式。多重次調和窮竭函式(plurisubharmonic ex-haustive function)多複變函數論中一類重要的實函式.設月是C”中的域，滬是月上的一個多重次調和函式，如果對每個實數。，有 則稱必是月上的一個多重次調和窮竭函式.
- 帶調和函式
帶調和函式 帶調和函式(zonal harmonic function)一類具有特殊性質的球面調和函式。由等式 確定的k次球面調和函式Z歲t'稱為以x'為極點的k次帶調和函式，其中交飛為k次球面調和函式類.Z歲 t的一個重要特性就是:對任一旋轉P，有
- 復變函式專題選講
1.1 調和函式及其序列 1.2 次調和函式 2 dirichlet 問題與調和測度 2.1 dirichlet 問題 2.2 green 函式 2.3 調和測度 第七章г函式和b 函式 1 г函式 1.1 г(z) 的積分定義 1.2 г(z) 的無窮乘積表示 1.3 г(z) 的線積分表示 1.4 stirling 公式 2 函式b(z,ζ)2.1 復變數b 函式的定義...
- 面調和函式
面調和函式 [1](surface harmonics)有時亦稱球函式.即拉普拉斯方程齊次多項式解的角向部分.將拉普拉斯方程在球坐標系(r, B),卯下的解寫成r'Y (B),卯的形式(n為正整數),Y (B),卯即為n次面調和函式.其中p為m階n次連帶勒讓德函式.在量子力學中,Yn <B,卯是角動量算符的本徵態,同時又是轉動群的不可...
- 立體調和函式
立體調和函式 立體調和函式(solid harmonics)拉普拉斯方程在直角坐標系下的n次齊次函式解.對於正整數n，存在2n+1個線性無關的n次立體調和函式.在球坐標系中寫出，即為r0Y,. (B,卯)，其中Yn＜B,卯為n次面調和函式.
- 復變函式論(2001年高等教育出版社出版的圖書)
《複變函數論》是2001年高等教育出版社出版的圖書，作者是張錦豪、邱維元。內容簡介 《複變函數論》從套用的角度出發，從現代數學的觀點介紹複分析的基礎知識與常用工具，還包括格林函式，貝格曼核，次調和函式等內容。《複變函數論》敘述清楚、精闢簡要，注重與數學分析的銜接，又著眼於與其他數學分支的聯繫。《復變...
- 橢球調和函式
由此容易推出： 定義在連通開集U上、使 |f|在U的一點達到其極大值的調和函式是常值函式(極大值原理)。C之開集U上的所有全純函式是調和的，它們的實部與虛部也是調和的。反之，如果U是C的單連通開集，則對任一實值調和函式f，存在U上的全純函式g，使Re(g)=f。極大值原理可推廣到稱為次調和函式的更一般...
- 函式論初步
9 廣義函式 9.1 形式傅立葉級數 9.2 H型和S型廣義函式 9.3 極限 10 Picard定理證明 10.1 Picard小定理 10.2 Picard大定理 11 多複變函數 11.1 基本性質 11.1.1 全純函式 11.1.2 開映射定理 11.2 解析開拓 11.2.1 全純函式從多圓柱邊界的開拓 11.2.2 Reinhardt域 11.3 次調和函式 11.3...
- 復變函式(1998年中國科技大學出版社出版的圖書)
中都有重要的套用.目錄 前言 第1章 複數與複變函數 第2章 全純函式 第3章 全純函式的積分表示 第4章 全純函式的 Taylor 展開及其套用 第5章 全純函式的 Laurent 展開及其套用 第6章 全純開拓 第7章 共形映射 第8章 調和函式與次調和函式 第9章 多復變數全純函式與全純映射 名詞索引 ...
- 調和空間
調和空間 調和空間(harmonic space)一種有序偶.所謂調和空間，是指由一個局部緊的豪斯多夫空間X和X上的一個滿足調和公理的超調和簇2l組成的有序偶(X,l).在調和空間的開集U(UCX)上，uEl(U)稱為超調和函式，u E -'(U)稱為亞調和函式，h E 0u (U) (o U) =0l (U) (仁一lU)稱為調和函式.
- 復變函式續論
本書是李銳夫，程其襄編《複變函數論》一書的繼續，包含複變函數理論中較深入、重要的內容，並給出詳盡的證明。全書分為八章，分別討論了最大模定理，正規族，保形映射，單葉函式，整函式的分解，整函式的值分布，Picard定理，亞純函式，調和函式、次調和函式等內容。本書可作為高等師範院校及綜合大學數學專業選修...
- 球調和函式
球調和函式 球調和函式(spherical harmonics function )球體調和函式與球面調和函式的總稱.R”上的k次齊次調和多項式稱為k次球體調和函式，它在單位球面上的限制稱為k次球面調和函式.所謂調和多項式指的是滿足拉普拉斯方程。
- 調和上屬
調和上屬是一個數學術語。調和上屬(harmonic majorant)函式值大於 或等於給定函式的調和函式.設f和h均為區域D 上的函式，h調和且hf(相應地，hf)，則稱h是 f的調和上屬(相應地，調和下屬).D上的一個上調 和函式若有調和下屬，則它必有最大的調和下屬. 調和上屬習慣上也稱調和強函式，調和下屬也 稱調和弱...
- 球函式
由此容易推出： 定義在連通開集U上、使 |f|在U的一點達到其極大值的調和函式是常值函式(極大值原理)。C之開集U上的所有全純函式是調和的，它們的實部與虛部也是調和的。反之，如果U是C的單連通開集，則對任一實值調和函式f，存在U上的全純函式g，使Re(g)=f。極大值原理可推廣到稱為次調和函式的更一般...
- 過分函式
由此容易推出： 定義在連通開集U上、使 |f|在U的一點達到其極大值的調和函式是常值函式(極大值原理)。C之開集U上的所有全純函式是調和的，它們的實部與虛部也是調和的。反之，如果U是C的單連通開集，則對任一實值調和函式f，存在U上的全純函式g，使Re(g)=f。極大值原理可推廣到稱為次調和函式的更一般...
- 不變調和函式
不變調和函式 不變調和函式，是拉普拉斯一貝爾特拉米方程。不變調和函式(invariant harmonic function)拉普拉斯一貝爾特拉米方程。u=。的解。記K(z,z)為C”中有界域D的伯格曼核函式，則由伯格曼核決定的伯格曼度量為 互為逆方陣.D上二階連續可微實值函式f(z,z)稱為不變調和函式，如果△f=0.
- 多復變函式論基礎
第一章 多復變數全純函式 §1.1 全純函式 §1.2 多圓柱的Cauchy積分公式及其套用 §1.3 Hartogs現象 §1.4 球和球面上的積分 §1.5 次調和函式和Hartogs定理 §1.6 Riemann可去奇點定理和Rado定理 註記 第二章 全純映射 §2.1 全純映射的導數 §2.2 單葉全純映射 §2.3 H.Cartan定理和球的...
- 機率位勢論
機率位勢論（probability potential theory）是研究位勢論與機率論的內在聯繫的新數學分支。簡介 機率位勢論是研究位勢論與機率論的內在聯繫的新數學分支。發展 20世紀四五十年代，杜布(Doob,J.L.)、角谷靜夫等人發現了經典位勢論與布朗運動的深刻聯繫。1954年，杜布的論文“半鞍與次調和函式”被公認為是開創了...
- 多元複分析
《多元複分析》是 2015年3月科學出版社出版的圖書，作者是塗振漢。簡介 多元複分析是現代數學中非常活躍的學科之一，其內容廣泛、發展迅速，本書是學習多遠複分析的基本教材。全書共8章，全純函式與全純映照、延拓定理、復解析集，全純域、次調和函式與多重次調和函式、e運算元的存在性定理和L2方法等。出版時間 2015...
- 掃除空間論
1954年，杜布的論文“半鞍與次調和函式”被公認為是開創了機率與位勢聯繫的研究的新篇章。20世紀50年代中期以後，亨特(Hunt,G.A.)等人進一步把它推廣到相當一般的馬爾可夫過程，給出更具普遍意義的“位勢”的定義。從此，位勢論的許多概念、性質獲得了明確的機率意義，而分析工具的引人大大促進了機率論的深入發展...
- 多複分析
mapping）。多複分析的產生源自於該學科與單複分析若干本質差異的發現，如Poincare、Hartogs的發現。基本概念如全純域、多次調和函式等；經典問題如Levi問題，Cousin I、II問題（單復變Weierstrass, Mittag-Leffler相應問題的推廣）等；與代數、幾何、分析緊密相關的重要方法如層論， 方程的L 方法，積分表示等。
- 複分析導論(第一卷)
《複分析導論（第一卷）》是2011年出版的圖書，作者是（俄羅斯）沙巴特。內容介紹 《複分析導論(第1卷)·單複變函數(第4版)》文字敘述極具特色，素材豐富，內容包括全純函式及其性質、解析延拓、幾何理論的基礎、解析方法、調和與次調和函式等。《複分析導論(第1卷)·單複變函數(第4版)》可供高等學校數學、...
- 模群
黎曼曲面上定義的函式稱為解析的(或調和的或次調和的)，如果在每個參數鄰域內它表示為局部參數的解析函式(或調和或次調和函式)。緊緻黎曼曲面稱為閉黎曼曲面，否則為開黎曼曲面。黎曼曲面理論中具有基本的重要性的定理是單值化定理。同胚 同胚是拓撲空間之間的一種變換。若f是拓撲空間(X，T)到(Y，U)的單滿映射...
