基本介紹
- 中文名:正則變換
- 外文名:canonical transformation
- 套用學科:力學
- 適用領域範圍:天體力學
- 實質:保持正則形式不變的變數的變換
- 用途:用來尋找可略坐標
定義

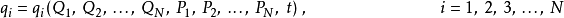
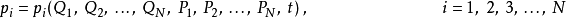


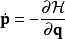
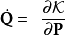
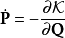
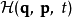
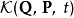
實際用處



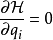

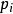

生成函式方法
- 主項目:正則變換生成函式
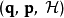
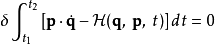
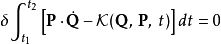
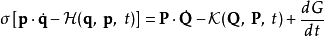
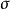
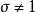
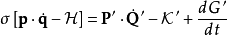
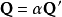
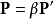

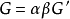
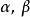
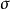


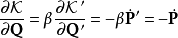
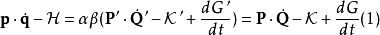

第一型
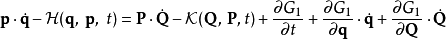

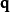


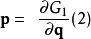
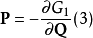

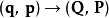


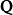
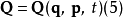

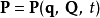

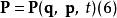
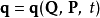
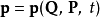

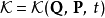
第二型

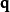
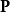

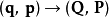

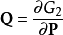

第三型

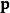

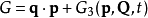
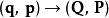
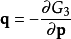


第四型

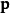

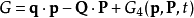
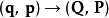
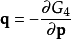




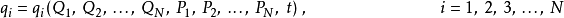
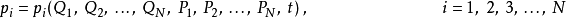


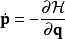
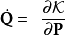
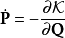
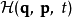
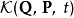



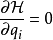

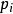

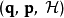
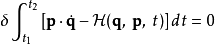
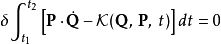
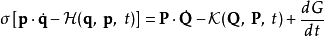
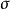
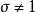
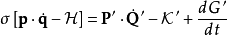
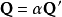
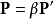

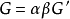


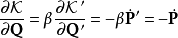
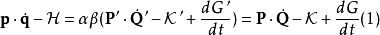

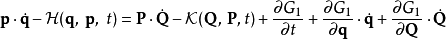



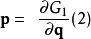
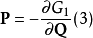

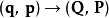


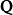
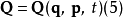

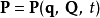

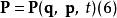
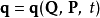
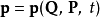

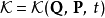

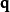
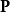

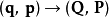

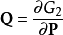


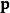

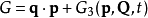
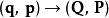
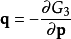



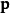

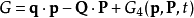
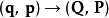
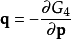


正則變換是由一組正則變數到另一組能保持正則形式不變的變數的變換。在哈密頓力學裡,正則變換(canonical transformation)是一種正則坐標的改變,(q,p)-->(Q,P)...
在哈密頓力學裡,當計算正則變換時,生成函式扮演的角色,好似在兩組正則坐標之間的一座橋。為了要保證正則變換的正確性 ,採取一種間接的方法,稱為生成函式方法。...
變換理論是研究天體運動方程的一種處理方法。在天體力學中﹐經常需要將變數進行變換﹐從而改變天體運動方程的形式以便於研究。根據不同的問題﹐需要研究採用什麼樣的...
勒讓德變換(英語:Legendre transformation)是一個在數學和物理中常見的技巧,得名於阿德里安-馬里·勒壤得(Arien-Marie Legendre)。該操作是一個實變數的實值凸...
其優點是:不僅新舊變數之間的變換具有顯函式的形式,同時其結果在正則變換之下保持不變,因此它與用哪一組正則變數進行計算無關,而具有通用性。 電子計算機的創製和...
他首先將月球的攝動函式展開成四百多個三角項,然後進行一系列的正則變換,使每次變換都能消去其中的一項。他花了差不多二十年的時間,總共進行了上千次變換,找到...
其優點是:不僅新舊變數之間的變換具有顯函式的形式,同時其結果在正則變換之下保持不變,因此它與用哪一組正則變數進行計算無關,而具有通用性。...
2 數學性質 ▪ 標度性質 ▪ 平移性質 ▪ 反演性質 ▪ 線形變換性質 3 套用 ▪ 熱力學 ▪ 經典力學 ▪ 正則變換 4 參閱 勒...
全書分7章,主要內容包括:分析力學形成前夕和初期的動力學方程及方法;拉格朗日動力學;多自由度力學體系的微振動;哈密頓動力學;正則變換;泊松括弧與拉格朗日括弧;哈密...
李炳照,男,1975 年生,博士,北京理工大學數學學院副教授,碩士生導師。主要從事小波變換、分數階Fourier 變換、線性正則變換等新穎數學方法的基本理論及其在非平穩信號...
攝動問題可分為正則攝動和奇異攝動兩類形式。如果令 ε=0,Γε的表達式可化為Γ0,而且是一致有效的,就稱這個攝動問題是正則攝動問題。如果在Sε中令ε=0...
乙部內容共分8章:第-1章講述變分法;第2章講述Hamilton原理與最小作用量原理;第3、4章講述Hamilton正則方程式和正則變換;第5章講述古典力學中的時間可逆性;第6...
