基本介紹
- 中文名:勒讓德變換
- 外文名:Legendre transformation
- 命名來源:阿德里安-馬里·勒壤得
- 套用:經典力學
概述



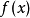

為方便討論,把討論限定在





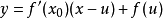






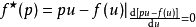
定義
最大值式定義








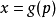


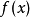







反函式式定義






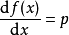





套用
熱力學


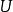

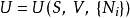


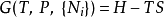



經典力學


正則變換







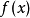






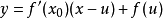






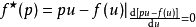








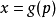


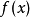













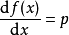







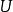

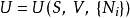


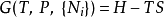








勒讓德變換(英語:Legendre transformation)是一個在數學和物理中常見的技巧,得名於阿德里安-馬里·勒壤得(Arien-Marie Legendre)。該操作是一個實變數的實值凸...
法國數學家、天文學家勒讓德(Legendre, Asrien-Marie,1752-1833)出生在一個比較富有的家庭,從小受到良好的教育。18歲時,通過了數學物理的畢業論文答辯。...
阿德利昂·瑪利·埃·勒讓德(公元1752年9月18日- 1833年1月10日)為法國數學家,生於巴黎,卒於同地。約1770年畢業於馬扎蘭學院。1775年任巴黎軍事學院數學教授...
伴隨勒讓德多項式(Associated Legendre polynomials,又譯締合勒讓德多項式、連帶勒讓德多項式、關聯勒讓德多項式)是數學上對常微分方程解函式序列的稱呼,在數學和理論...
拉格朗日量則是E上的jet叢(射流叢)J上的函式;取拉格朗日量的纖維內的勒讓德變換就產生了一個時間上的對偶叢的函式,其在t的纖維是餘切空間T*Et,它有一個自然...
今天,人們就稱這樣的變換為勒讓德變換,勒讓德變換的概念實際上出現得比對偶空間或共軛空間的概念還要早,應該說,後一概念的起源之一就是勒讓德變換。20世紀50...
對於簡單可壓縮系統,通過勒讓德變換可以得到包括內能在內的4個特徵函式U、F、H和G,由此可得四類相關方程。如函式的定義式、微分式、麥氏關係等。對含有n種廣義...
又把勒讓德變換進一步抽象為共軛函式的概念。因此,今天人們又把函式到其共軛函式的變換稱為勒讓德-芬切爾變換。 [1] 共軛級數共軛級數詳細定義 編輯 共軛級數(...
為元素的 N×N 矩陣,做勒讓德變換令 ,η 稱為矩,二階歐拉-拉格朗日方程轉換化為一階方程組這個方程組稱為典範方程組或哈密頓方程組,H 稱為哈密頓函式。...
已知有幾個證明,一個正在使用的事實是,正均勻、凸實值函式的勒讓德變換是緊湊凸集的(凸)指標函式。許多作者將支撐函式限制在歐幾里德單位球體上,並將其視為Sn-...
拉格朗日量則是E上的jet叢(射流叢)J上的函式;取拉格朗日量的纖維內的勒讓德變換就產生了一個時間上的對偶叢的函式,其在t的纖維是餘切空間TEt,它有一個自然的...
凸共軛是勒讓德變換的一種推廣;凸共軛也被稱作Legendre–Fenchel變換,或者Fenchel變換(以Adrien-MarieLegendre和WernerFenchel命名)。 ...
切觸變換的理論(也即保持一個切觸結構的變換)是索甫斯·李發展的,其目的是雙重的,包括研究微分方程(例如勒讓德變換)和表述射影對偶性中常見的'空間元素的變換...
熱函是內能和體積的勒讓德變換。它是SpN總合的熱勢能。 [1] 目錄 ●基本信息 ●基本解釋 熱函基本信息 編輯 【詞目】熱函...
麥克斯韋關係的方程組的四個等式分別來自四個不同的熱力學方程。這四個方程可以通過對熱力學主方程做勒讓德變換而得到。中文名 麥克斯韋關係式 類別 物理化學 ...
哈密頓量 可以通過對拉格朗日量進行勒讓德變換得到。哈密頓量是經典力學的另一種表述哈密頓力學的基礎。拉格朗日量可以視為定義在所有廣義坐標可能值組成的組態空間的...
M是橢圓型或雙曲型仿射球面的充分必要條件為f的勒讓德變換函式:滿足:其中L1為仿射平均曲率,它為常數.歐氏曲面論中法線交於一點或互相平行的曲面中有球面和平面...
兩組變數之間的變換可以通過勒讓德變換得到。對於具有s個自由度的系統,其廣義坐標、廣義速度、廣義動量的個數均為s,L與H則分別包含2s+1個變數。(各函式變數均...
焓是內能和體積的勒讓德變換。它是SpN總合的熱勢能。 [1] 克勞修斯-克拉佩龍方程參見 編輯 范特霍夫方程 安托萬方程 參考資料 1. Wark, Kenneth. Generalized...
深入研究了均勻系熱力學參量和特徵量勒讓德變換的對偶對稱性,給出對稱變換的完整關係;系統研究了各種曲線擺諧振動嚴格等時性的條件,並給出一些曲線擺嚴格等時振動的...
4.勒讓德(Legendre)變換5.熱力學函式6.內能與熵的表達式索引·收起全部<<物理學與偏微分方程前言 編輯 很多重要的物理、力學學科,其基本方程均是偏微分方程。...
拉格朗日量則是E上的jet叢(射流叢)J上的函式;取拉格朗日量的纖維內的勒讓德變換就產生了一個時間上的對偶叢的函式,其在t的纖維是餘切空間TEt,它有一個自然的...
有時對方程(22)可使用勒讓德變換Χ=y┡,Y=xy┡-y將方程變形。此變換的逆變換也具有同樣的形式:;稱為對稱原理。當兩方程F(x,y,p)=0與F(P,ΧP-Y,Χ...
1.4 勒讓德變換1.5 哈密頓原理與哈密頓正則方程1.6 互等定理第2章 彈性力學基本方程與變分原理2.1 應力分析2.2 應變分析2.3 應力一應變關係2.4 彈性力學的...
有效作用量 為 的勒讓德變換:,其中 由方程 決定。 也是單粒子不可約格林函式的生成泛函。如果將 寫成經典場 (稱為背景場)和量子場 的疊加:...
