概念簡述
拉格朗日力學是
分析力學中的一種,於1788年由
約瑟夫·拉格朗日所創立。拉格朗日力學是對
經典力學的一種的新的理論表述,著重於數學解析的方法,是分析力學的重要組成部分。
力學系統由一組坐標來描述。比如一個
質點的運動(在笛卡爾坐標系中)由x,y,z三個坐標來描述。一般的,N個質點組成的力學系統由3N個坐標來描述。力學系統中常常存在著各種約束,使得這3N個坐標並不都是獨立的。力學系統的獨立坐標的個數稱之為
自由度。對於N個
質點組成的力學系統,若存在m個約束,則系統的自由度為
 拉格朗日力學
拉格朗日力學S = 3N − m
哈密爾頓量H可以通過對
拉格朗日量進行
勒讓德變換得到。哈密爾頓量是經典力學的另一種表述哈密爾頓力學的基礎。拉格朗日量可以視為定義在所有
廣義坐標可能值組成的組態空間的
切叢上的函式,而哈密爾頓量是相對應的
餘切叢上的函式。哈密爾頓量在量子力學中到處出現(參看哈密爾頓量 (量子力學))。
1948年,
費曼發明了
路徑積分表述,將最小作用原理擴展到量子力學。在該表述中,
粒子穿過所有可能的始態和終態的所有路徑;特定終態的機率是所有可能導向它的軌跡的機率之和。在經典力學的範圍,路徑積分表述簡單的退化為
哈密爾頓原理。
 拉格朗日力學
拉格朗日力學相關信息
人物簡介
拉格朗日1736年1月25日生於義大利西北部的
都靈。父親是法國陸軍騎兵里的一名軍官,後由於經商破產,家道中落。據拉格朗日本人回憶,如果幼年是家境富裕,他也就不會作數學研究了,因為父親一心想把他培養成為一名律師。拉格朗日個人卻對法律毫無興趣。
 拉格朗日力學
拉格朗日力學 到了青年時代,在數學家雷維里的教導下,拉格朗日喜愛上了幾何學。17歲時,他讀了英國天文學家哈雷的介紹
牛頓微積分成就的短文《論分析方法的優點》後,感覺到“分析才是自己最熱愛的學科”,從此他迷上了數學分析,開始專攻當時迅速發展的數學分析。
18歲時,拉格朗日用義大利語寫了第一篇論文,是用牛頓
二項式定理處理兩函式乘積的高階微商,他又將論文用拉丁語寫出寄給了當時在柏林科學院任職的數學家
歐拉。不久後,他獲知這一成果早在半個世紀前就被萊布尼茲取得了。這個並不幸運的開端並未使
拉格朗日灰心,相反,更堅定了他投身數學分析領域的信心。
 拉格朗日
拉格朗日1755年拉格朗日19歲時,在探討
數學難題“
等周問題”的過程中,他以歐拉的思路和結果為依據,用純分析的方法求變分
極值。第一篇論文“極大和極小的方法研究”,發展了
歐拉所開創的
變分法,為變分法奠定了理論基礎。變分法的創立,使
拉格朗日在都靈聲名大震,並使他在19歲時就當上了都靈皇家炮兵學校的教授,成為當時歐洲公認的第一流數學家。1756年,受歐拉的舉薦,拉格朗日被任命為普魯士科學院通訊院士。
1764年,
法國科學院懸賞徵文,要求用
萬有引力解釋月球
天平動問題,他的研究獲獎。接著又成功地運用微分方程理論和近似解法研究了科學院提出的一個複雜的六體問題(木星的四個衛星的運動問題),為此又一次於1766年獲獎。
1766年德國的腓特烈大帝向拉格朗日發出邀請時說,在“歐洲最大的王”的宮廷中應有“歐洲最大的數學家”。於是他應邀前往柏林,任
普魯士科學院數學部主任,居住達20年之久,開始了他一生科學研究的鼎盛時期。在此期間,他完成了《
分析力學》一書,這是
牛頓之後的一部重要的經典力學著作。書中運用
變分原理和分析的方法,建立起完整和諧的力學體系,使力學分析化了。他在序言中宣稱:力學已經成為分析的一個分支。
1783年,
拉格朗日的故鄉建立了"都靈科學院",他被任命為名譽院長。1786年腓特烈大帝去世以後,他接受了法王
路易十六的邀請,離開柏林,定居巴黎,直至去世。
這期間他參加了巴黎科學院成立的研究法國
度量衡統一問題的委員會,並出任法國米制委員會主任。1799年,法國完成統一度量衡工作,制定了被世界公認的長度、面積、體積、質量的單位,拉格朗日為此做出了巨大的努力。
1791年,拉格朗日被選為
英國皇家學會會員,又先後在巴黎
高等師範學院和巴黎綜合工科學校任數學教授。1795年建立了法國最高學術機構——法蘭西研究院後,拉格朗日被選為科學院數理委員會主席。此後,他才重新進行研究工作,編寫了一批重要著作:《論任意階數值方程的解法》、《解析函式論》和《函式計算講義》,總結了那一時期的特別是他自己的一系列研究工作。
1813年4月3日,
拿破崙授予他帝國大十字勳章,但此時的拉格朗日已臥床不起,4月11日早晨,拉格朗日逝世。
人物成就
拉格朗日科學研究所涉及的領域極其廣泛。他在數學上最突出的貢獻是使
數學分析與幾何與力學脫離開來,使數學的獨立性更為清楚,從此數學不再僅僅是其他學科的工具。拉格朗日總結了18世紀的數學成果,同時又為19世紀的數學研究開闢了道路,堪稱法國最傑出的數學大師。同時,他的關於月球運動(三體問題)、行星運動、
軌道計算、兩個不動中心問題、流體力學等方面的成果,在使天文學力學化、力學分析化上,也起到了歷史性的作用,促進了力學和
天體力學的進一步發展,成為這些領域的開創性或奠基性研究。
 拉格朗日力學
拉格朗日力學在柏林工作的前十年,拉格朗日把大量時間花在
代數方程和
超越方程的解法上,作出了有價值的貢獻,推動了
代數學的發展。他提交給柏林科學院兩篇著名的論文:《關於解數值方程》和《關於方程的代數解法的研究》。把前人解三、四次代數方程的各種解法,總結為一套標準方法,即把方程化為低一次的方程(稱輔助方程或預解式)以求解。
在數論方面,拉格朗日也顯示出非凡的才能。他對
費馬提出的許多問題作出了解答。如,一個
正整數是不多於4個
平方數的和的問題等等,他還證明了圓周率的無理性。這些研究成果豐富了數論的內容。
在《解析函式論》以及他早在1772年的一篇論文中,在為
微積分奠定理論基礎方面作了獨特的嘗試,他企圖把
微分運算歸結為
代數運算,從而拋棄自
牛頓以來一直令人困惑的
無窮小量,並想由此出發建立全部
分析學。但是由於他沒有考慮到
無窮級數的收斂性問題,他自以為擺脫了
極限概念,其實只是迴避了極限概念,並沒有能達到他想使微積分代數化、嚴密化的目的。不過,他用
冪級數表示函式的處理方法對分析學的發展產生了影響,成為實變函式論的起點。
拉格朗日也是
分析力學的創立者。拉格朗日在其名著《
分析力學》中,在總結歷史上各種力學基本原理的基礎上,發展
達朗貝爾、
歐拉等人研究成果,引入了勢和
等勢面的概念,進一步把數學分析套用於
質點和
剛體力學,提出了運用於靜力學和動力學的普遍方程,引進
廣義坐標的概念,建立了
拉格朗日方程,把力學體系的
運動方程從以力為基本概念的
牛頓形式,改變為以能量為基本概念的分析力學形式,奠定了分析力學的基礎,為把力學理論推廣套用到物理學其他領域開闢了道路。
 拉格朗日力學
拉格朗日力學 拉格朗日的研究工作中,約有一半同
天體力學有關。他用自己在
分析力學中的原理和公式,建立起各類天體的
運動方程。在
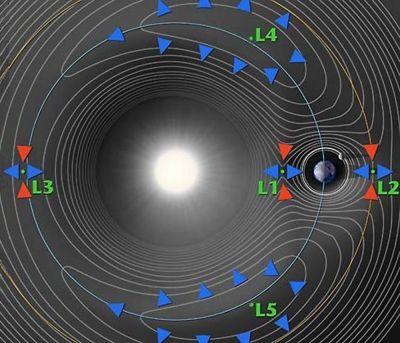
天體運動方程的解法中,拉格朗日發現了三體問題運動方程的五個特解,即拉格朗日
平動解。此外,他還研究了彗星和小行星的
攝動問題,提出了彗星起源假說等。
近百餘年來,數學領域的許多新成就都可以直接或間接地溯源於拉格朗日的工作。所以他在數學史上被認為是對分析數學的發展產生全面影響的數學家之一。被譽為“歐洲最偉大的數學家”。
坐標
在矢量力學中,約束的存在體現於作用於系統的約束力。約束力引入額外的未知量,通常使問題變得更為複雜。但若能選取適當的s個完全滿足約束條件的獨立坐標,則約束不再出現在問題中,只需要求解關於s個未知變數的方程,使問題得以大大簡化。這樣的s個坐標不再局限於各
質點的位置坐標,而可以是任何能描述系統的幾何參量,因此稱為“
廣義坐標”。
 拉格朗日力學
拉格朗日力學假設
格朗日力學的一個基本假設是:具有n個
自由度的系統,其
運動狀態完全由n個廣義坐標及它們的
微商(廣義速度)決定。或者說,力學系統的運動狀態由一個廣義坐標和廣義速度的函式描述:
拉格朗日方程
其中Q為所對應的非保守的
廣義力。 拉格朗日方程的地位等同於
牛頓力學中的牛頓第二定律。但具有更普遍的意義。
概念拓展
1948年,
費曼發明了
路徑積分表述,將
最小作用量原理擴展到量子力學。在該表述中,
粒子穿過所有可能的始態和終態的所有路徑;特定終態的機率是所有可能導向它的軌跡的機率之和。在經典力學的範圍,路徑積分表述簡單的退化為
哈密頓原理。
 拉格朗日力學
拉格朗日力學 拉格朗日力學
拉格朗日力學 拉格朗日力學
拉格朗日力學 拉格朗日
拉格朗日 拉格朗日力學
拉格朗日力學 拉格朗日力學
拉格朗日力學 拉格朗日力學
拉格朗日力學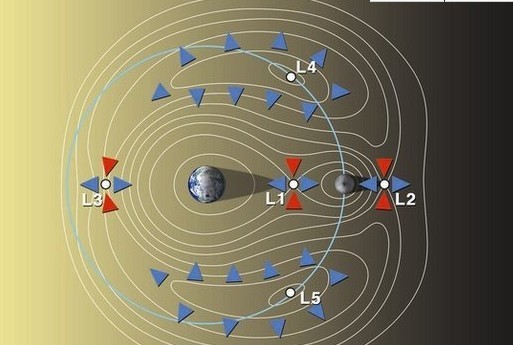
 拉格朗日力學
拉格朗日力學 拉格朗日力學
拉格朗日力學 拉格朗日力學
拉格朗日力學 拉格朗日
拉格朗日 拉格朗日力學
拉格朗日力學 拉格朗日力學
拉格朗日力學 拉格朗日力學
拉格朗日力學