達朗貝爾原理(D'Alembert's principle)是求解約束系統動力學問題的一個普遍原理,由法國數學家和物理學家J.達朗貝爾於1743年提出。
達朗貝爾在《動力學》一書中,提出了達朗貝爾原理,與牛頓第二定律相似,但其發展在於可以把動力學問題轉化為靜力學問題處理,還可以用平面靜力的方法分析剛體的平面運動,這一原理使一些力學問題的分析簡單化,而且為分析力學的創立打下了基礎。達朗貝爾還對當時運動量度的爭論提出了自己的看法,他認為兩種量度是等價的,並提出了物體動量的變化與力的作用時間有關。達朗貝爾第一次用微分方程表示場,同時提出了著名的達朗貝爾原理——流體力學的一個原理,雖然存在一些問題,但是達朗貝爾第一次提出了流體速度和加速度分量的概念。達朗貝爾的力學知識為天文學領域做出了重要貢獻。同時達朗貝爾發現了流體自轉時平衡形式的一般結果,關於地球形狀和自轉的理論。
基本介紹
- 中文名:達朗貝爾原理
- 外文名:D'Alembert's principle
- 表達式:F+N+(-Ma)=0
- 提出者:達朗貝爾
- 提出時間:1743
- 套用學科:物理
- 適用領域範圍:力學
原理的表述
原理的意義
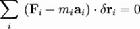 達朗貝爾原理簡化公式
達朗貝爾原理簡化公式
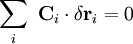 達朗貝爾原理公式
達朗貝爾原理公式