基本介紹
概述
簡史
宇宙觀
始於17世紀
 車輛動力學
車輛動力學18世紀牛頓第二定律
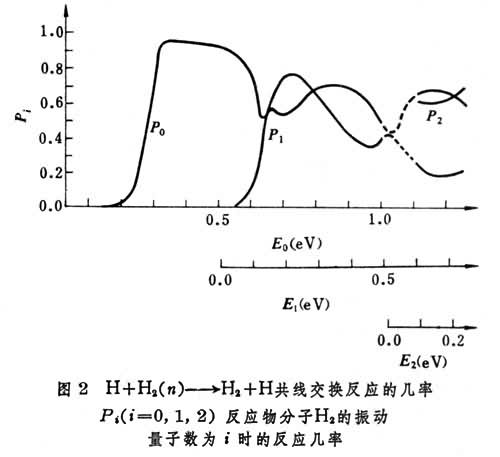 分子反應動力學
分子反應動力學19世紀漢密爾頓正則方程
內容
兩個抽象模型
兩類基本內容
動力學普遍定理
剛體
達朗貝爾原理
套用
 天體地球動力學
天體地球動力學
 車輛動力學
車輛動力學 分子反應動力學
分子反應動力學 天體地球動力學
天體地球動力學動力學是理論力學的一個分支學科,它主要研究作用於物體的力與物體運動的關係。動力學的研究對象是運動速度遠小於光速的巨觀物體。動力學是物理學和天文學的基礎,...
團體動力學(英文:group dynamics),又稱群體動力學、集團力學,是研究諸如群體氣氛、群體成員間的關係、領導作風對群體性質的影響等群體生活的動力方面的社會心理學分支...
結構動力學分析是CAE分析的主要內容之一。結構動力分析不同於靜力分析,常用來確定時變載荷對整個結構或部件的影響,同時還要考慮阻尼及慣性效應的作用。...
藥物動力學是一門較年輕的新興藥學與數學間的邊緣科學,是近20年來才獲得的迅速發展的藥學新領域。藥物動力學是研究藥物在動物體內的含量隨時間變化規律的科學,是...
系統動力學(簡稱SD—system dynamics)的出現於1956年,創始人為美國麻省理工學院(MIT)的福瑞斯特(J.W.Forrester)教授。系統動力學是福瑞斯特教授於1958年為分析生產...
反應動力學是研究各種物理、化學因素(如溫度、壓力、濃度、反應體系中的介質、催化劑、流場和溫場分布、停留時間分布等)對反應速率的影響以及相應的反應機理和數學...
化學動力學(chemical kinetics),也稱反應動力學、化學反應動力學,是物理化學的一個分支,是研究化學過程進行的速率和反應機理的物理化學分支學科。它的研究對象是性質...
運動力學在傳統物理學中是一個空白。運動是宇宙最基本的現象,天體的運動突出表現為公轉和自轉,在簡易論中,運動還包括天體軌道的移動。運動力學通常指物體的運動,...
酶動力學是研究酶結合底物能力和催化反應速率的科學。研究者通過酶反應分析法(enzyme assay)來獲得用於酶動力學分析的反應速率數據。...
一級動力學(first-order kinetic)是藥動學概念,按藥物轉運速度與藥雖或濃度之間的關係,藥物在體內的消除速率過程可分為一級、零級和米氏速率過程。一級動力學...
分子動力學是一門結合物理,數學和化學的綜合技術。分子動力學是一套分子模擬方法,該方法主要是依靠牛頓力學來模擬分子體系的運動,以在由分子體系的不同狀態構成的...
套用系統動力學的基本理論和DYNAMO語言建立的仿真模型。系統動力學模型可用於巨觀經濟和微觀經濟。...
心理動力學(psychodynamic),又稱精神動力學或精神分析學。根據心理動力學的觀點,行為是由強大的內部力量驅使或激發的。...
航天動力學是研究太空飛行器和運載器在飛行中所受的力及其在力作用下的運動的科學,又稱星際航行動力學。航天動力學研究的運動包括太空飛行器的質心運動,稱軌道運動;太空飛行器...
空氣動力學是力學的一個分支,研究飛行器或其他物體在同空氣或其他氣體作相對運動情況下的受力特性、氣體的流動規律和伴隨發生的物理化學變化。它是在流體力學的基礎...
細胞動力學是研究生物系統或人工系統中細胞群體的來源、變化、分布和運動規律,以及研究各種條件對這些過程如何影響的一門科學。研究細胞發生、命運決定與細胞再生、分化...
《運動學與動力學》是2011年電子工業出版社出版的圖書,作者是汪越勝。本書重點介紹了最具有理論力學課程特點的基本內容,以不同層次和角度論述了基本概念、基本公式和...
動力學規律提示的事物之間的規律性關係,是一種一一對應的確定的關係,它指明一種事物的存在必定導致另一種確定事物的發生,偶然現象可以忽略不計。統計學規律揭示的不...
《物理動力學》是1999年世界圖書出版公司出版的圖書,作者是E.M.Lifshitz/等 。...... 《物理動力學》是1999年世界圖書出版公司出版的圖書,作者是E.M.Lifshitz/等...
該書為理論力學教材的續編,包括分析力學、運動穩定性、剛體動力學、有心力場中的運動、多體系統動力學等五部分內容。該書可作為工程力學專業的本科生教材,或作為對...
《分析動力學》是2012年出版的圖書,作者是陳濱。...... 《分析動力學(第2版)》(作者陳濱)系統、全面地論述分析動力學。除包括有傳統的經典內容外,還包括了近幾...
電極動力學指的是電極過程動力學,電極過程動力學組成部分研究電極反應進程甲電極界面及其近旁所發生的各種過程的動力學行為。包括電化學反應器即各類電池中的電極過程,...
《動力學基礎》是2003年10月江蘇河海大學出版的圖書,作者是武清璽。...... 《動力學基礎》是2003年10月江蘇河海大學出版的圖書,作者是武清璽。書名 動力學基礎 ...
