歐拉動力學方程是剛性動力學的重要方程。剛性動力學是一般力學的一個分支,研究剛體在外力作用下的運動規律。它是機器部件的運動,艦船、飛機、火箭等航行器的運動以及天體姿態運動的力學基礎。
基本介紹
- 中文名:歐拉動力學方程
- 性質:剛性動力學的重要方程
- 類別:力學的一個分支
- 研究範圍:剛體在外力作用下的運動規律
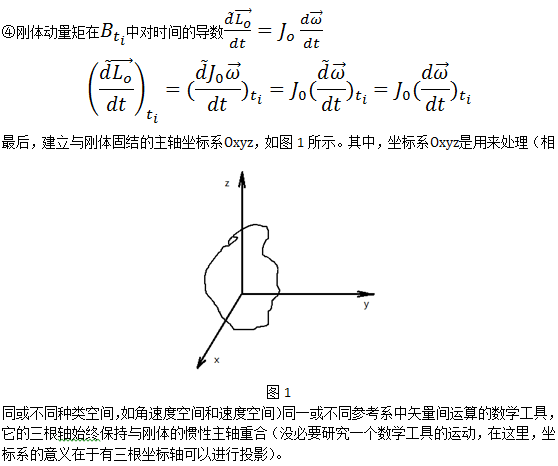
歐拉動力學方程是剛性動力學的重要方程。剛性動力學是一般力學的一個分支,研究剛體在外力作用下的運動規律。它是機器部件的運動,艦船、飛機、火箭等航行器的運動以及天體姿態運動的力學基礎。
歐拉動力學方程是剛性動力學的重要方程。剛性動力學是一般力學的一個分支,研究剛體在外力作用下的運動規律。它是機器部件的運動,艦船、飛機、火箭等航行器的運動以及...
歐拉運動學方程是描述剛體運動的微分方程,在剛體繞定點運動中,反映角速度和歐拉角關係的方程,該方程在剛體繞定點運動的研究中有重要地位。...
歐拉方程,即運動微分方程,屬於無粘性流體動力學中最重要的基本方程,是指對無粘性流體微團套用牛頓第二定律得到的運動微分方程。歐拉方程套用十分廣泛。1755年,瑞士...
為了便於計算物理量在流場中的分布,一般多採用歐拉變數。氣體動力學基本方程組...動量、能量的變化率,根據基本物理定律寫出的方程組就是積分形式的流體力學方程組...
歐拉動力學方程是剛體動力學的基本方程,剛體定點轉動動力學則是動力學中的經典理論。陀螺力學的形成說明剛體動力學在工程技術中的套用具有重要意義。多剛體系統動力學...
工程中剛體的定點轉動多發生於繞相交軸轉動的場合,如研磨機、雷達天線、三軸模擬平台、機械臂等,可用動量矩定理或歐拉動力學方程建立運動方程並求解。陀螺的近似理論...
歐拉-拉格朗日方程 目錄 1 簡介 2 套用 3 參考文獻 拉格朗日方程簡介 拉格朗日方程:對於完整系統用廣義坐標表示的動力方程,通常系指第二類拉格朗日方程,是法國數學...
此時可建立著名的剛體繞固定點轉動的歐拉動力學方程組:結合在一起,就構成了求解剛體繞固定點轉動的封閉的運動微分方程組。它是由六個一階非線性微分方程所組成。...
流體動力學方程組(hydrodynamic equation system)描述流體運動的基本方程組.運動流體狀 態可用速度二一(二二,二,,二二),密度P和壓力p五個變 數描述,它們都是...
中文名:歐拉方程 本質:運動微分方程 地位:無粘性流體動力學最重要的方程 首次提出:1755年 領域:物理學 方程形式:ax²D²+bxD+c)y=f(x)簡介...
“流體動力學基本方程”是將質量、動量和能量守恆定律用於流體運動所得到的聯繫流體速度、壓力、密度和溫度等物理量的關係式。對於系統和控制體都可以建立流體動力學...
在經典電動力學中,將描述電磁波的勢所滿足的一個微分方程組稱作達朗貝爾方程(英文:d'Alembert equation)。達朗貝爾方程是一個非齊次的波動方程。...
歐拉-伯努利梁方程(英語:Euler–Bernoulli beam theory),是一個關於工程力學、經典梁力學的重要方程;是一個簡化線性彈性理論用於用於計算梁受力和變形特徵。歐拉-...
歐拉差分法(Eulerian difference methods)一類偏微分方程數值解法,指利用歐拉坐標系,從歐拉形式流體動力學方程出發的求解流體力學問題的差分方法的總稱。...
他還給出剛體在重力作用下,繞旋轉對稱軸上的定點轉動(拉格朗日陀螺)的歐拉動力學方程的解,對三體問題的求解方法有重要貢獻,解決了限制性三體運動的定型問題。...
伯努利方程就是一個關於工程力學、古典棟樑力學的重要方程;是一個簡化線性彈性理論且能計算棟樑受力和變形特微的。歐拉─伯努利棟樑方程約成形於1750年,但這條方程...
多剛體系統的動力學牛頓–歐拉法 編輯 將系統拆成單個的質點或剛體,用矢量力學的方法分別建立動力學方程(見剛體動力學),再補充反映剛體之間約束的運動學方程,組成...
《可壓縮流與歐拉方程(英文版)》主要考慮三維空間中,其初值在單位球面外為常值的任意狀態方程的經典可壓縮歐拉方程。當初值與常狀態差別適當小時,我們建立的定理...
歐拉情形(Eider condition)亦稱歐拉一潘索情形.任意初條件下剛體繞定點運動可獲得...這種情形的動能T和對固定點的動量矩G都恆定,因而降低了動力學方程的階數,可用...
瀏覽一下數學和物理教科書的索引就會找到如下查照:歐拉角(剛體運動)、歐拉常數(無窮級數)、歐拉方程(流體動力學)、歐拉公式(複合變數)、歐拉數(無窮級數)、歐拉多...
第一章介紹分析力學的基本概念、動力學普遍方程和拉格朗日方程。第二章有選擇地...在第四章中,著重介紹剛體定點運動的運動學和動力學的基本知識,以及歐拉情形和...
結構動力學簡要概述 早在18世紀後半葉,瑞士的丹尼爾第一·伯努利(見伯努利家族)首先研究了稜柱桿側向振動的微分方程。瑞士的L.歐拉求解了這個方程並建立了計算稜柱...
這就是L.歐拉於1758年得出的剛體定點運動的微分方程,稱為歐拉動力學方程。歐拉動力學方程和歐拉運動學方程聯立,在已知外力矩、、和初始條件(三個歐拉角的初值和...
將歐拉動力學方程同歐拉運動學方程(見歐拉角)結合在一起,就構成求解剛體定點轉動的封閉的運動微分方程組。它是由6個一階非線性微分方程組成;從中消去ω′x、ω′...
