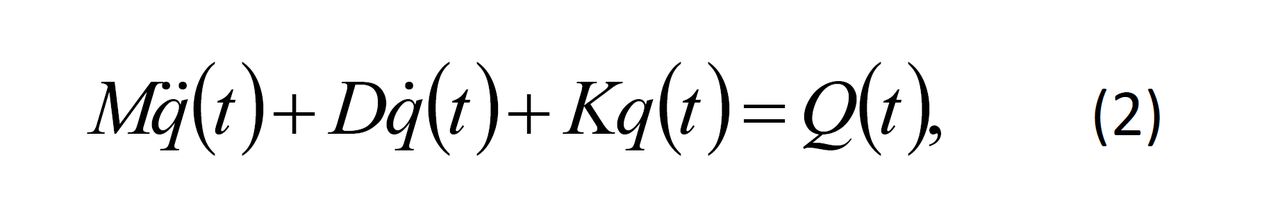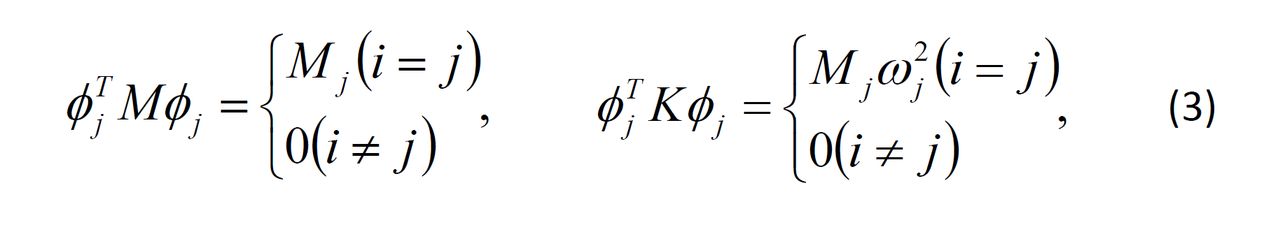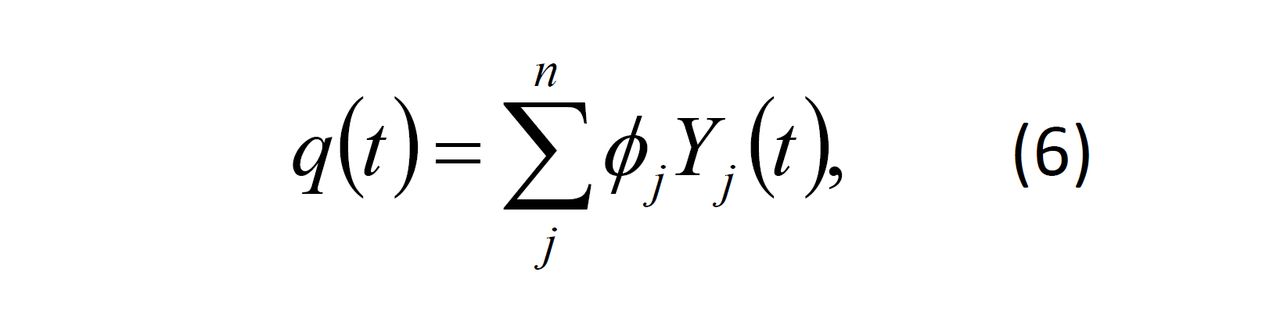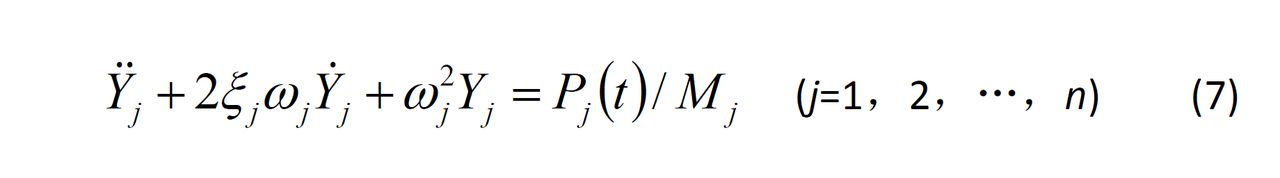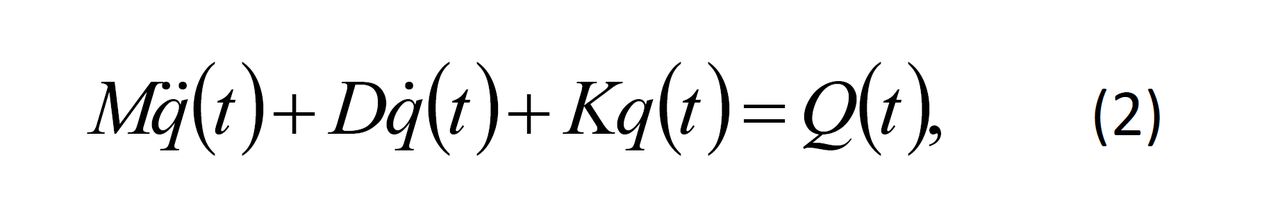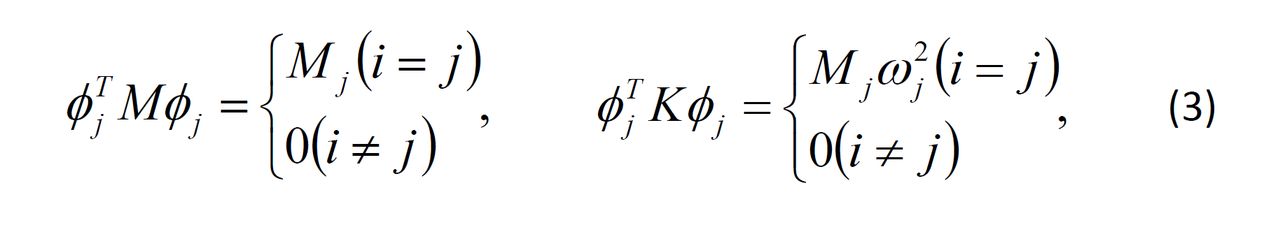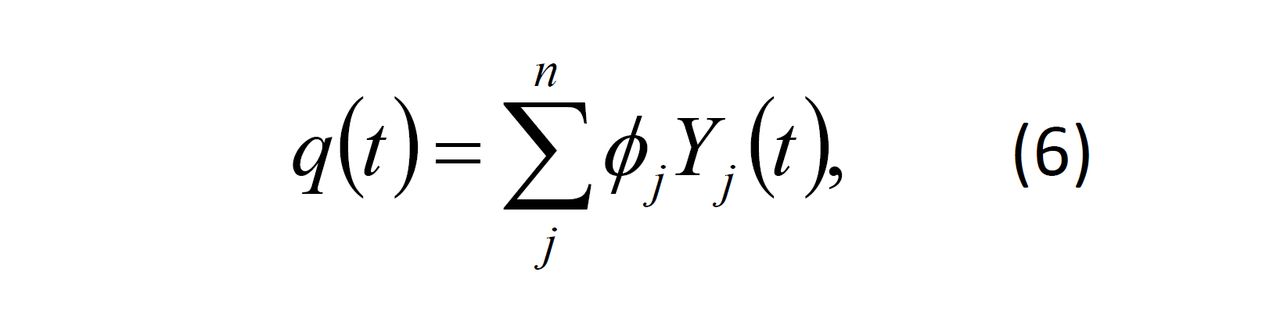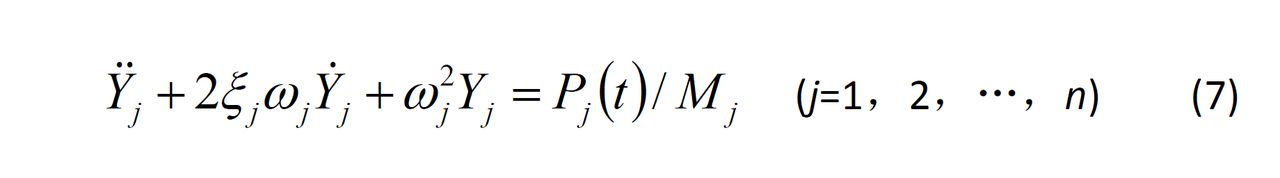結構動力學是研究結構在動力荷載作用下的振動問題。在動力荷載作用下，其一要考慮慣性力影響，其二考慮位移、內力、速度、加速度均隨時間變化而變化。
基本介紹
- 中文名：結構動力學
- 外文名：structuraldynamics
- 領域：力學，結構
- 適用領域：土木，機械，運輸、航空航天等
- 研究內容：動載荷作用下結構的動力反應
- 起源：18世紀後半葉
簡介,研究內容,實驗研究,理論分析,發展情況,簡要概述,新的問題,
簡介
結構動力學研究在動態荷載作用下的結構內力和位移的計算理論及方法。與結構靜力計算相比，結構承受周期荷載、衝擊荷載、隨機荷載等動力荷載作用時，結構的平衡方程中必須考慮慣性力的作用，有時還要考慮阻尼力的作用，且平衡方程是瞬時的，荷載、內力、位移等均是時間的函式。
在結構動力計算中要考慮慣性力、阻尼力的作用，故必須研究結構的質量在運動過程中的自由度。動力自由度是指結構運動過程中任一時刻確定全部質量的位置所需的獨立幾何參數的數目。
靜力計算考慮的是結構的靜力平衡，荷載、約束力、位移等都是不隨時間變化的常量。動力問題與靜力問題相比較，在結構動力計算中，需要考慮慣性力，荷載是時間的函式，需要考慮慣性力。在動力問題中，根據達朗貝爾原理，建立包含慣性力的動力平衡方程，這樣就把動力學問題化成瞬間的靜力學問題．運用靜力學方法計算結構的內力和位移。與靜力平衡方程不同，動力平衡微分方程的解(即動力反應)是隨時間變化的，因而動力分析比靜力分析更加複雜。
研究內容
結構動力學的研究內容包括實驗研究和理論分析兩個方面。
實驗研究
在18～19世紀，大量的實驗研究不僅為理論分析奠定了基礎，而且成為當時解決實際工程問題的主要手段。例如，19世紀對橋樑和路軌在移動載荷作用下的回響所作的實驗，曾對鐵路運輸工程的發展作出重要貢獻。即使在理論分析已較為完善的今天，實驗仍不可缺少。20世紀60年代，美國在研製土星V運載火箭時就不惜耗費50萬美元，製作一個1/10的動力相似模型，以測定其動力特性。至於材料和結構阻尼特性的測定、振動環境試驗等工作，則主要依靠實驗研究。
結構動力學實驗中有以下幾個課題：①材料性能的測定：包括測定動態應力－應變曲線、衝擊載荷作用下的極限強度(見材料的力學性能)、重複載荷作用下的疲勞強度(見疲勞)、材料或結構的阻尼特性等;②結構動力相似模型的研究：包括各種情況下的動力相似條件、相似模型的設計和製作等;③結構固有(自由)振動參量的測定:對結構或其相似模型施加一定方式的激勵，如頻率可調的簡諧力、衝擊力或隨機力，然後根據回響確定結構的固有頻率、振動形態(振型)以及振型阻尼係數等參量；④振動環境試驗：在現場或在能模擬振動環境的試驗台上對結構或其相似模型進行振動試驗，用以確定結構的工作可靠性或使用壽命；⑤其他專業性試驗。
理論分析
結構的質量是一連續的空間函式，因此結構的運動方程是一個含有空間坐標和時間的偏微分方程，只是對某些簡單結構，這些方程才有可能直接求解。對於絕大多數實際結構，在工程分析中主要採用數值方法。作法是先把結構離散化成為一個具有有限自由度的數學模型，在確定載荷後，導出模型的運動方程，然後選用合適的方法求解。
（1）教學模型
將結構離散化的方法主要有以下三種：①集聚質量法：把結構的分布質量集聚於一系列離散的質點或塊，而把結構本身看作是僅具有彈性性能的無質量系統。由於僅是這些質點或塊才產生慣性力，故離散系統的運動方程只以這些質點的位移或塊的位移和轉動作為自由度。對於大部分質量集中在若干離散點上的結構，這種方法特別有效。②瑞利－里茲法(即廣義位移法)：假定結構在振動時的位形(偏離平衡位置的位移形態)可用一系列事先規定的容許位移函式fi(它們必須滿足支承處的約束條件以及結構內部位移的連續性條件)之和來表示，例如，對於一維結構，它的位形u(x)可以近似地表為：
式中的qj稱為廣義坐標，它表示相應位移函式的幅值。這樣，離散系統的運動方程就以廣義坐標作為自由度。對於質量分布比較均勻，形狀規則且邊界條件易於處理的結構，這種方法很有效。③有限元法：可以看作是分區的瑞利－里茲法，其要點是先把結構劃分成適當數量的區域(稱為單元)，然後對每一單元施行瑞利－里茲法。通常取單元邊界上(有時也包括單元內部)若干個幾何特徵點(例如三角形的頂點、邊中點等)處的廣義位移qj作為廣義坐標，並對每個廣義坐標取相應的插值函式作為單元內部的位移函式(或稱形狀函式)。在這樣的數學模型中，要求形狀函式的組合在相鄰單元的公共邊界上滿足位移連續條件。一般地說，有限元法是最靈活有效的離散化方法，它提供了既方便又可靠的理想化模型，並特別適合於用電子計算機進行分析，是目前最為流行的方法，已有不少專用的或通用的程式可供結構動力學分析之用。
（2）載荷確定
載荷有三個因素，即大小，方向和作用點。如果這些因素隨時同緩慢變化，則在求解結構的回響時，可把載荷作為靜載荷處理以簡化計算。載荷的變化或結構的振動是否“緩慢”，只是一個相對的概念。如果載荷的變化周期在結構自由振動周期的五、六倍以上，把它當作靜載荷將不會帶來多少誤差。若載荷的變化周期接近於結構的自由振動周期，即使載荷很小，結構也會因共振(見線性振動)而產生很大的回響，因而必須用結構動力學的方法加以分析。
動載荷按其隨時間的變化規律可以分為：①周期性載荷，其特點是在多次循環中載荷相繼呈現相同的時間歷程，如旋轉機械裝置因質量不平衡而引起的離心力。周期性載荷可藉助傅立葉分析分解成一系列簡諧分量之和。②衝擊載荷，其特點是載荷的大小在極短的時間內有較大的變化。衝擊波或爆炸是衝擊載荷的典型來源。③隨機載荷，其時間歷程不能用確定的時間函式而只能用統計信息描述。由大氣湍流引起的作用在飛行器上的氣動載荷和由地震波引起的作用在結構物上的載荷均屬此類。對於隨機載荷，需要根據大量的統計資料制定出相應的載荷時間歷程(載荷譜)。對於前兩種載荷，可以從運動方程解出位移的時間歷程並進一步求出應力的時間歷程。對於隨機載荷，只能求出位移回響的統計信息而不能得到確定的時間歷程，因而須作專門分析才能求出應力回響的統計信息。
在結構動力學分析中，動載荷的確定是一項重要而困難的工作。近年來發展的“載荷識別”是一項新技術，它根據結構在實標工作情況下測得的回響資料反推結構所受到的載荷資料。
（3）運動方程
可用三種等價但形式不同的方法建立，即：①利用達朗伯原理引進慣性力，根據作用在體系或其微元體上全部力的平衡條件直接寫出運動方程；②利用廣義坐標寫出系統的動能、勢能、阻尼耗散函式及廣義力表達式，根據哈密頓原理或其等價形式的拉格朗日方程導出以廣義坐標表示的運動方程；③根據作用在體系上全部力在虛位移上所作虛功總和為零的條件，即根據虛功原理導出以廣義坐標表示的運動方程。對於複雜系統，套用最廣的是第二種方法。
通常，結構的運動方程是一個二階常微分方程組，寫成矩陣形式為：
式中q(t)為廣義坐標矢量，是時間t的函式，其上的點表示對時間的導數；M、D、K分別為對應於q(t)的結構質量矩陣、阻尼矩陣和剛度矩陣，Q(t)是廣義力矢量。
（4）方程解法
運動方程(2)可用振型疊加法或逐步積分法求解。
①振型疊加法 先求出結構作自由振動時的固有頻率和振型，然後利用求得的振型作為廣義位移函式再對運動方程作—次坐標變換，進而求出方程的解。
一個n個自由度的結構具有n個固有頻率ωj和n個振型φj(j=1，2，…，n)。φj規定了n個廣義坐標qi(i=1，2，…，n)在第j個振型中的相對大小。振型滿足下列關係式：
式中上標“T”為矩陣轉置符號；Mj為第j個振型的廣義質量。i≠j時的關係式稱為振型的正交條件。正交條件在物理上意味著不同的振型之間不存在能量交換，即結構在作自曲振動時各個振型都是獨立進行的。振型疊加法可以有條件地用於有阻尼的情況。若結構的阻尼矩陣可表為：
D=αK+βM， (4)
式中α和β是常數，則稱之為比例阻尼矩陣。對應的振型滿足
式中ξj稱為第j個振型的阻尼係數。同時，有阻尼的自振頻率將改變為
條件(4)還可放寬為
，式中
為M的逆矩陣。
通過振型及相應的廣義坐標Yj(t)，可將方程(2)中的廣義坐標矢量q(t)表示為：
代入方程(2)，並左乘以，利用正交條件(3)和(5)，可將方程(2)轉化為：
式中Pj(t)=φj-Q(t)是對應於第j個振型的廣義力。方程(7)可以通過時域分析法或頻域分析法求解。時域分析法是利用卷積積分給出方程(7)的解，可用於任意變化的載荷情況。頻域分析法是利用傅立葉分析把周期性載荷展開為一系列簡諧分量之和，然後計算結構對每一簡諧分量的回響，最後疊加各簡諧回響項而獲得結構的總回響。這種方法適用於周期性載荷情況。對於非周期性載荷，也可以利用傅立葉變換技術。1965年出現了快速傅立葉變換——一種用計算機計算離散傅立葉變換的方法，它在效率和功能方面的優點，使得頻域分析方法能和傳統的時域分析方法相媲美，並正在引起結構動力學領域的變革。
由於運動方程(7)可以逐個獨立地求解，使得振型疊加法具有很大的優越性，因而它已成為結構動力學中一個套用最廣泛的分析方法。對於大多數類型的動載荷，各個振型的回響是不同的，一般是頻率最低的振型回響最大，高頻振型的回響則趨向減小，因而在疊加過程中只需要計及頻率較低的若干項，若得到的回響已達到精度要求，就可捨棄頻率較高的各項，從而可以大大減少計算工作量。振型疊加法只適用於線性振動問題。
②逐步積分法 可用於直接求解耦合的運動方程(2)，而且對阻尼矩陣的性質不需要附加任何限制，也適用於使振型疊加法失效的非線性結構系統的動力分析，因此是一種普遍適用的方法。該法是把時間劃分為一系列很短的時段，按照初始條件確定初始時刻的廣義位移q和廣義速度，通過運動方程(2)解出廣義加速度，然後可設在這一時段內為常量，通過積分求出在這一時段結束時刻的q和值，並以它們作為下一時段的初始值，如此一步一步求解下去，就能得到最終的結果。如果結構是非線性系統，同樣可假設結構參量(如剛度)在每一時段內是常量並取為該時段開始時刻的瞬時參量值。逐步積分法是一種近似的方法，為了減小積累誤差，必須把時段取得非常短，因而其計算工作量很大。為了提高效率，可以假設加速度在每一時段內為線性函式(或其他簡單函式)。這樣，即使取時段(即積分步長)為運動周期的十分之一甚至五分之一也可以得到合理的結果。
發展情況
簡要概述
早在18世紀後半葉，瑞士的丹尼爾第一·伯努利(見伯努利家族)首先研究了稜柱桿側向振動的微分方程。瑞士的L．歐拉求解了這個方程並建立了計算稜柱桿側向振動的固有頻率的公式。1877～1878年間，英國的瑞利發表了兩卷《聲學理論》，書中具體地討論了諸如桿、梁、軸、板等彈性體的振動理論，並提出了著名的瑞利方法(或稱瑞利原理)。1908年瑞士的w．里茲提出了一個求解變分問題的近似方法，後來被稱作瑞利－里茲法。這個方法實際上推廣了瑞利方法，在很多學科中(包括結構動力學在內)發揮了巨大的作用。1928年，S．P．鐵木辛柯發表了《工程中的振動問題》一書，總結了彈性體振動理論及其在工程中套用的情況。近幾十年來，由於工程實踐的需要和科學探索的興趣，人們進行了大量的實驗和理論研究工作，使這門學科在實踐和理論分析上都獲得了高度的發展。
新的問題
二百多年來，結構動力學已經發展成為一門比較成熟的學科。但是，結構動力學仍在探索新的問題，如：
（1）復模態理論 傳統的結構動力學主要以不考慮阻尼或只考慮比例阻尼系統的振型的純模態理論為基礎，近年來在考慮任意阻尼的復模態理論研究方面已取得一定的進展。深入開展復模態理論的研究將進一步推動結構力學的理論分析方法和實驗技術的發展。
（2）主動振動控制 研究結構動力學的最終目的是要控制振動，防止因振動而造成的損害，而利用其有利的特性。傳統的作法是根據結構動力回響的分析結果，在必要時對結構採取相應的修改措施，這是一種被動的振動控制方式。航空界在20世紀60年代開始發展主動控制技術，即根據振動感測器所獲得的結構振動信息，通過控制系統加以分析並操縱若干小型操縱面，以達到降低飛機對大氣湍流的回響水平或推遲顫振發生的目的，這是一種主動的振動控制方式。振動控制由被動發展到主動，是結構動力學中一個值得注意的動向。
（3）最佳化設計 結構動力學中的傳統作法是分析已有結構的動力特徵，其逆問題——設計一個結構使其具有預定的動力特性——越來越引起了人們的重視(見結構最佳化設計)。
（4）跨學科和其他問題 吸收其他學科的新技術，改善現有的方法和技術以提高它們的效率和精度，並開展跨學科的研究工作。
