剛體的定點運動所屬現代詞,指的是剛體上某一點始終保持不動的一種運動。
基本介紹
- 中文名:剛體的定點運動
- 屬性:現代詞
- 解釋:剛體上某一點始終保持不動的
- 接解釋:一種運動
正文
歐拉角 作定點運動的剛體有三個自由度。通常取如下定義的三個歐拉角作為確定剛體位置的獨立參數。建立一個固結在剛體上的動坐標系和一個以定點為原點的定坐標系(圖2)。定坐標系的坐標平面和動坐標系的坐標平面的交線稱為節線。和軸的夾角稱為剛體的自轉角;和軸之間的夾角稱為進動角;軸和軸之間的夾角稱為剛體的章動角。、、都叫做歐拉角,因此,剛體定點運動的運動方程可用三個歐拉角的時間函式來表示:
 剛體的定點運動
剛體的定點運動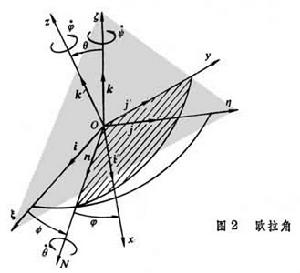 剛體的定點運動
剛體的定點運動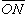 剛體的定點運動
剛體的定點運動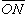 剛體的定點運動
剛體的定點運動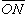 剛體的定點運動
剛體的定點運動本體極面 定點運動的剛體的任何有限位移可用繞過定點的某軸的一次轉動而達到。因此,剛體每一瞬時運動都可看成是繞通過定點的某一瞬時轉軸所作的瞬時轉動,這一瞬時轉軸就是該瞬時剛體角速度矢量的方向軸(圖3),在此瞬時轉軸上的每一點的速度都是零。瞬時轉軸在隨剛體運動的空間中所描繪出的錐面稱為本體極面。瞬時轉軸在固定空間中所描繪出的錐面稱為空間極面。剛體定點運動可用幾何方法描述為,本體極面在空間極面上作無滑動的滾動。
歐拉運動學方程 剛體作定點運動的角速度矢量
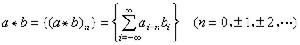 剛體的定點運動
剛體的定點運動 剛體的定點運動
剛體的定點運動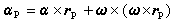 剛體的定點運動
剛體的定點運動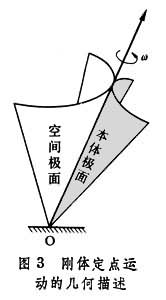 剛體的定點運動
剛體的定點運動此三個方程稱為歐拉運動學方程。
歐拉動力學方程 如取過定點O 的剛體的三個互相垂直的慣量主軸(見慣量張量)為坐標系的坐標軸,並設剛體對這三個坐標軸的主轉動慣量分別為、、。外力系對點的主矩矢量在這三個軸上的投影分別為、、,則定點運動的剛體的運動微分方程為
這就是L.歐拉於1758年得出的剛體定點運動的微分方程,稱為歐拉動力學方程。歐拉動力學方程和歐拉運動學方程聯立,在已知外力矩、、和初始條件(三個歐拉角的初值和它們的初始導數值)下,可積分求得剛體定點運動的運動方程,就知道了三個歐拉角隨時間變化的規律。在任意外力系的作用和任意形狀剛體的情況下,這一組方程至今沒有得到用求積形式表示的精確解。困難主要來自方程的非線性。但因剛體定點運動的理論分析在陀螺技術中具有重要作用,所以這個問題的解決仍然是剛體動力學的重大研究課題之一。這一組方程,目前只在下述三種特殊情況下得到了精確解:
① 歐拉-潘索情況。作用於剛體上的外力的合力通過固定點O,則、、都恆為零。此時剛體繞定點作慣性轉動,歐拉動力學方程簡化為
1851年L.潘索給這個情況下所得的解作了著名的幾何解釋:剛體運動可看成剛體關於O點的慣量橢球在一固定平面上的無滑動的滾動,此固定平面稱為潘索平面(圖4)。
② 拉格朗日-泊松情況。J.L.拉格朗日於1788年給出了另一種特殊情況下的解,S.-D.泊松於1813年對此情況又作了進一步研究。他們所研究的情況是:剛體只受重力作用,重心在O軸上,剛體關於O點的慣量橢球是旋轉橢球,即=的情況。如重心離O點的距離為,則在此情況下歐拉動力學方程簡化為
③柯瓦列夫斯卡婭情況。1888年俄國科學家С.Β.柯瓦列夫斯卡婭利用複變函數論的觀點給出了第三種情況下的解。在此情況下:剛體只受重力作用,重心在剛體關於O點的慣量橢球的赤道平面內,離O點的距離為,且==2。此時歐拉動力學方程為
這裡動坐標系的軸通過重心。
 剛體的定點運動
剛體的定點運動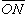 剛體的定點運動
剛體的定點運動 剛體的定點運動
剛體的定點運動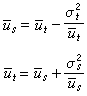 剛體的定點運動
剛體的定點運動 剛體的定點運動
剛體的定點運動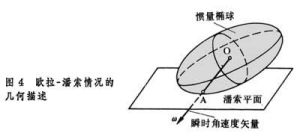 剛體的定點運動
剛體的定點運動 剛體的定點運動
剛體的定點運動 剛體的定點運動
剛體的定點運動