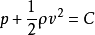定律內容
牛頓運動定律包含以下三個定律:
孤立質點保持靜止或做勻速直線運動;
用公式表達為:
,式中
為合力,
為速度,
為時間。
動量為
的質點,在外力
的作用下,其動量隨時間的變化率同該質點所受的外力成正比,並與外力的方向相同;用公式表達為:
。
若質點的質量不隨時間變化(即
),則質點運動的加速度的大小同作用在該質點上的外力的大小成正比,加速度的方向和外力的方向相同;用公式表達為:
。
相互作用的兩個質點之間的作用力和反作用力總是大小相等,方向相反,作用在同一條直線上;
用公式表達為:
(式中
表示質點2受到的質點1的作用力,
表示質點1受到的質點2的反作用力)。
(艾薩克·牛頓在《自然哲學的數學原理》中,對該定律的原始表述與上述表述幾乎完全一致;書中還給出了基於以上定律的六條推論。牛頓運動定律的分量形式及在如自然坐標系等其它坐標系下的形式詳見各子詞條。該定律在各版本教材中被引用時,其形式亦可能被改變。) 定律特點
牛頓第一運動定律為後續定律準備了概念並定性闡明了
力和
運動的關係。特別地,第一定律中所述的“物體不受
外力作用時的運動狀態”和第二定律中的物體所受外力矢量和為零(
合力為零)這一運動狀態不同,不能把第一定律當成第二定律在
時的特殊情況,因為
肯定導出
加速度 ,但
的運動只能由第一定律本身徹底闡明其為慣性運動(
靜止或
勻速直線運動)。第一定律是完全獨立的基本定律,用其解決的問題,別的任何規律都無法解決,第二、第三定律根本不能取代第一定律。
牛頓第二運動定律引入了
慣性質量,全面完整地刻畫了物體因受力作用而產生加速度,以及加速度與
外力及
質量的定量關係,構成了第二定律獨立於第一、第三定律的深刻內涵和根本原因。
牛頓第三運動定律不能由第二定律推演得出,第二定律也代替不了第三定律,第一定律更不能取代第三定律;第三定律也是在非基於伽利略先前提出的觀點的基礎上,牛頓所提出的一條定律。第三定律的正確性要靠大量實踐來檢驗。第三定律其實是用力的語言表達的
動量守恆定律,而動量守恆定律是自然界中普遍成立的少量幾條基本物理規律之一,
動量守恆在任何物理領域中均成立(計及
電磁場的
動量後,運動電子與電磁場的動量也守恆)。
牛頓運動定律在研究對象上呈遞進關係。第一、第二定律只研究單一物體(可以只有一個物體,也可以從眾多物體中隔離出一個物體來作為研究對象),解決其不受力或受很多力作用後的運動問題;第三定律擴展了研究對象,至少研究是兩個物體之間的相互作用,這種相互作用制約或影響了研究對象或研究對象以外的其它物體的運動。只有把第一、第二和第三定律有機結合才能解決全部的複雜
動力學問題,由質點的動力學出發去解決
質點系、
剛體、
流體、
振動、
波動等的
力學問題。
牛頓運動定律都只在第一定律確定的
慣性參考系成立。牛頓的
絕對時空觀中的慣性系雖然存在邏輯循環(或稱邏輯同一)之難,但是在動力學的力的語言表達中是理論體系必不可少的。一切動力學問題確定了慣性系便能解決。由於任何科學都不可能做到絕對真理,力學也是一門近似程度比較高的科學,絕對的慣性系不存在,但近似的慣性系是始終存在。牛頓運動定律只在慣性系中適用,說明了三定律的一致性。
第一定律引入力的概念和闡明
慣性屬性,定性揭示力和運動的關係,為第二定律打下基礎、準備必要的概念;第三定律進一步給出作用力的性質,揭示物體運動的相互制約機制。三定律結合,全面解決了任意物體在受複雜的外力作用後的運動問題。牛頓運動定律是一個有機整體,是一脈相承的完整理論體系,是力學的基本公理,由它們出發推論而出的
動量定理、
動量守恆定律、
動能定理、
機械能守恆定律、
動量矩定理、
角動量守恆定律,進一步證實了動力學公理化體系相容性和一致性。
演繹驗證
| 方法概述 | 圖示 |
|---|
牛頓第一運動定律 |
伽利略的理想斜面實驗: |
牛頓第一運動定律存在邏輯同一之循環論證,可通過理想實驗對該定律進行理論推導。 現實中,當球沿斜面向下滾時速度增大,上滾時則減小。由此可知,球沿水平面滾動時,速度應不變。 但事實上由於存在 摩擦阻力,球速會越來越慢直至最後停下,且表面越 光滑球便會滾得越遠。由此可知,若沒有摩擦阻力,球將永遠滾下去。 若球沿一個光滑斜面從靜止狀態開始下滾,小球將滾上另一個斜面達到與原來的高度然後再下滾;減小斜面傾角後,小球在另一個斜面上仍達到同一高度但滾得遠些。由此可知,斜面平放時,球將永遠滾下去。 此即,力不是維持物體的運動(速度)的原因。一旦物體具有某一速度且不受外力,就將保持這一速度勻速直線地運動下去。 | 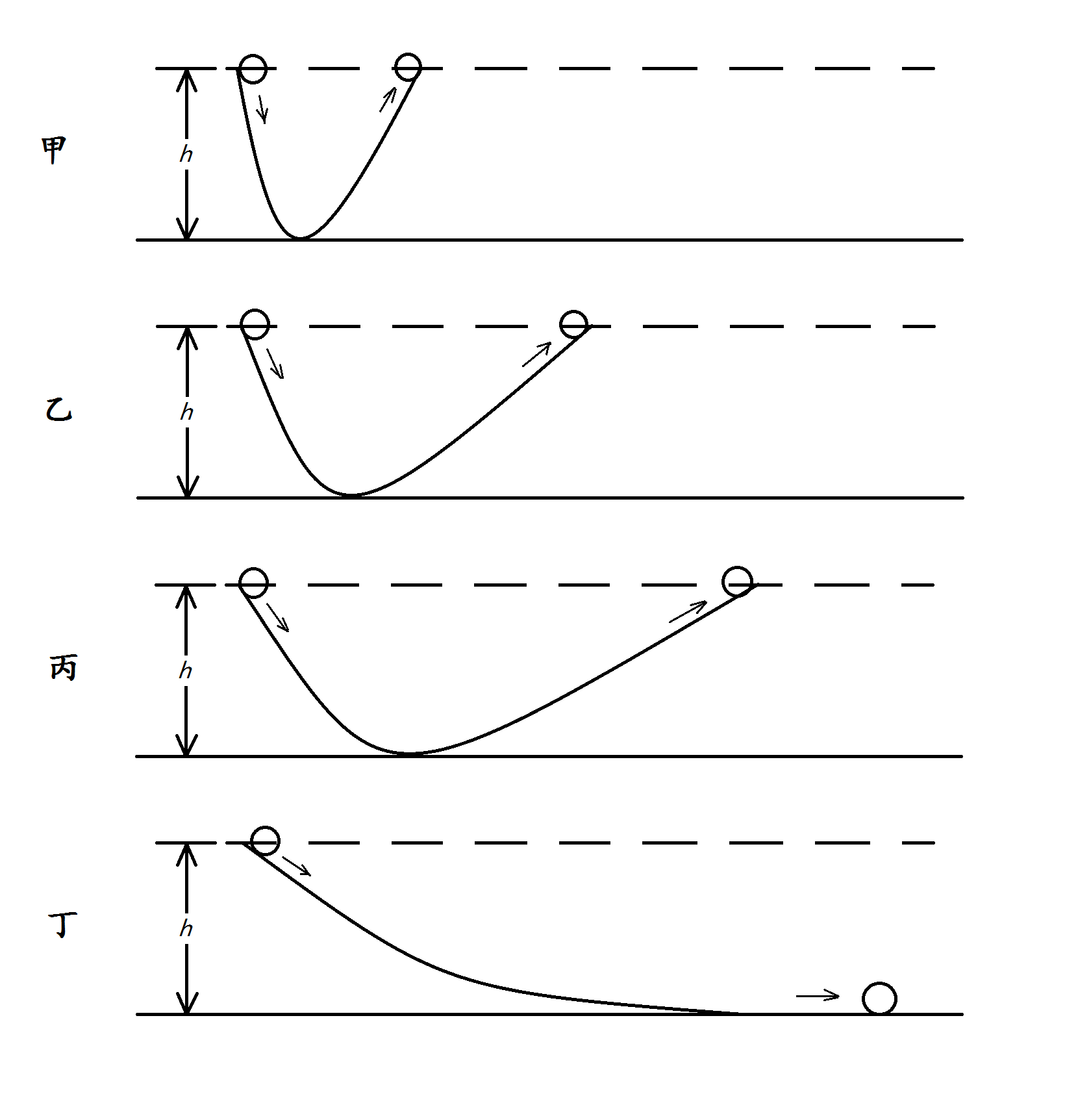 伽利略的理想斜面實驗 伽利略的理想斜面實驗 |
牛頓第二運動定律 |
用打點計時器驗證: |
研究系統的加速度與系統的質量和拉力間的關係時,將 打點計時器固定在木板的一端,把砝碼和小車栓在細線的兩端,細線跨過滑輪,砝碼的重量作為拉力,讓拖著紙帶的小車在平直的平面上運動,則小車及其上的砝碼、線的另一端栓著的鉤碼組成一個運動系統。 每次實驗均須在紙帶上註明拉力和系統的質量。 為了抵消摩擦力,通常採取如右圖所示的兩種方法:傾斜滑動法、水平拉線法。 | 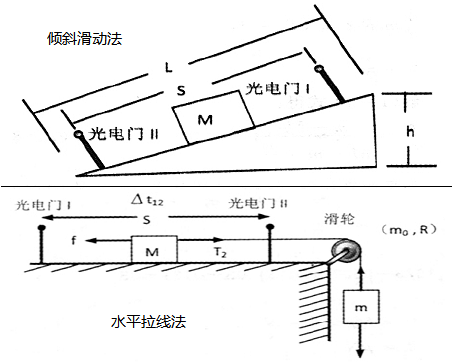 傾斜滑動法和水平拉線法 傾斜滑動法和水平拉線法 |
在氣墊導軌上驗證: |
將 氣墊導軌調平後(由於導軌都存在一定的彎曲,滑塊與導軌間存在阻力,所以調平在實驗中一般用滑塊通過兩個光電門時的速度相等來衡量),測出 粘性阻尼常數b。 為了修正粘滯性 摩擦阻力的存在所引起的速度損失,必須解決對粘滯性阻尼常數的測定。 為了消除粘滯性阻尼,通常採取以下兩種方法:傾斜導軌法(如右圖所示)、振動法。 |  傾斜導軌法 傾斜導軌法 |
用非線性回歸法驗證: |
即使是在氣墊導軌上驗證牛頓第二運動定律,也會有 空氣阻力作為主要影響因素影響實驗測量精度。這需要嘗試通過修正,其將影響減小到可忽略的程度。但常採用的 一元線性回歸法,不足以說明整個回歸方程的好壞;二元線性回歸法也同樣存在一定的問題。 用 非線性回歸法驗證定律,首先對質點運動的動力學模型進行線性化處理,得到模型的參數線性估計值,並以其作為 非線性模型的初值對動力學模型進行非線性回歸分析。 非線性回歸法驗證了定律的正確性,改進了驗證定律的傳統實驗方法,具有一定的套用和推廣價值。 |  牛頓第二運動定律非線性擬合圖 牛頓第二運動定律非線性擬合圖 |
|
牛頓第三運動定律 |
|
使用兩個 力感測器並保持兩個 感測器在同一平面上,讓兩個感測器的測力鉤相互鉤住或相抵。通過數據採集軟體,分別得到兩條力-時間圖線,如右圖1和圖 2所示;同時得到該時間段的 作用力和 反作用力隨時間變化的實時數據。 通過觀察可以看出作用力和反作用力與時間的對應關係:任意時刻,這兩個力的大小基本一致。這表示這兩個力的大小相等。 這種實驗方案,不僅適用於量化水平面上的 相互作用力,而且適用於量化豎直平面或與豎直方向成任意角度的同一平面上的相互作用力,只要和兩個力處於同一平面,就可以精確模擬作用力與反作用力,體現了兩個物體之間的作用力和反作用力總是大小相等,作用在同一直線上,更加直觀有效地突出牛頓第三運動定律的普適性。 |  感測器定量實驗 感測器定量實驗 |
|
取一根長約15厘米兩端開口的細玻璃管,管的直徑約3毫米(能使火柴進出)。
用兩根火柴裝入管中,使火柴頭在管的中間互相接觸,然後放平。用酒精燈對準火柴頭加熱、不久因玻璃管受熱升溫。火柴頭達到著火點迅速燃燒,氣體相互壓迫,兩根火柴桿從兩管的開口處同時飛出,並觀察到繼續燃燒。
由兩火柴頭飛出的路程大致相等,可說明物體間的作用力是相互的。此即直觀地驗證了牛頓第三運動定律。 | 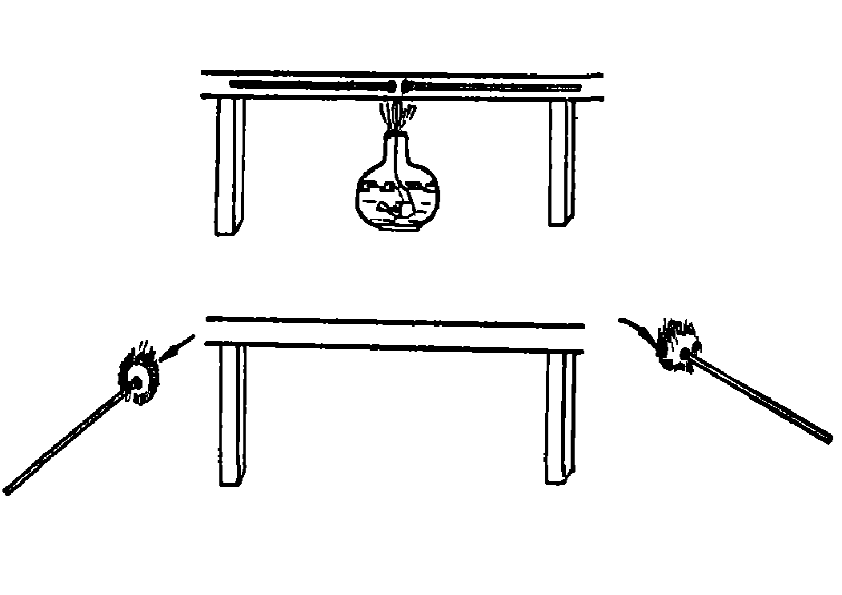 觀察法定性實驗 觀察法定性實驗 |
(牛頓運動定律的驗證性實驗有多種,本節僅挑選幾種重要或典型的實驗作為示例。隨著現代的實驗設施的利用,原來的實驗方法將有所改進或補充。)
適用條件
牛頓運動定律基於
牛頓力學的基本假設:①
空間是絕對的,可以認為是數學上的抽象空間,和空間內的填充物質無關;②
時間是連續的、均勻流逝的、無窮無盡的;③時間和空間無關;④時間和運動狀態無關;⑤物體的質量和物體的運動狀態無關。
廣義相對論在第一條假設上有突破,
狹義相對論突破了第三、四、五條假設。因此:
牛頓運動定律只適用於
質點,牛頓運動定律中所指的物體為質點。對
質點系,運用牛頓運動定律中的第二定律時一般採用
隔離法,或者採用質點系牛頓第二運動定律。對於作用力非
恆力的情形,如時間、速度或位置相關性的力,套用
積分等方法,牛頓運動定律亦可使用。
牛頓運動定律只適用於
慣性參考系。孤立質點相對它靜止或做勻速直線運動的
參考系為慣性參考系。在非慣性參考系中牛頓運動定律不適用,因為不受外力的物體在該參考系中也可能具有加速度,與牛頓第一運動定律相悖;只有在慣性參考系中牛頓運動定律才適用。但通過慣性力的引入可以使牛頓運動定律中的第二定律的表示形式在
非慣性系中適用,即使用力學方程
求解力學問題,式中
為在慣性系中測得的物體受的合力,
為在非慣性系中測得的慣性力(
為非慣性系統的加速度)。
牛頓運動定律只適用
巨觀問題。當考察的物體的運動線度可以和該物體的
德布羅意波相比擬時,由粒子運動
不確定性關係式可知,該物體的動量和位置已不能同時準確獲知,故牛頓動力學方程缺少準確的初始條件而無法求解,即經典的描述方法由於粒子運動不確定性關係式已經失效或者需要修改。對於一個作用量接近或小於
普朗克常量 的微觀粒子(亦或是一個
線度接近或小於
原子線度
的物體),必須使用
量子力學。量子力學用
希爾伯特空間中的態矢概念代替位置和動量(或速度)的概念來描述物體的狀態(即
波函式),用
薛丁格方程代替牛頓動力學方程(即含有
力場具體形式的牛頓第二運動定律)。用
態矢量代替
位置和
動量的原因是由
測不準原理而同時知道位置和動量的準確信息,但是可以知道位置和動量的機率分布;測不準原理對測量精度的限制就在於兩者的機率分布上有一個確定的關係。
牛頓運動定律具有
內在隨機性。其包含的“不確定行為”遠多於由它所給出的“確定行為”,特別是在
保守系統及
耗散系統中。
(牛頓運動定律中的三條定律各自獨立,各自存在適用範圍。各條定律不同表述的細微變化也會產生各自適用範圍的改變,具體的表述和對應拓廣形式的使用範圍可查閱各獨立詞條。)
發展簡史
公元前5世紀,古希臘哲學家
德謨克利特(Leucippus,公元前500—公元前440)、
伊壁鳩魯(Epicurus,公元前341—公元前270)認為:“當
原子在虛空里被帶向前進而沒有東西與他們碰撞時,它們一定以相等的速度運動。”這只是猜測或推想的結果。
公元前4世紀,古希臘哲學家
亞里士多德(
Aristotle,公元前384—公元前322)指出:靜止是物體的自然狀態,如果沒有作用力就沒有運動(
力是維持物體運動的原因)。該觀點遺失了“力能使物體停止運動,也能使物體開始運動”這一關鍵點,故錯誤。但他第一次提出了力與運動間存在關係,為力學發展做出了一定貢獻。
6世紀, 希臘學者菲洛彭諾斯(J.Philoponus)對亞里士多德的運動學說持批判態度。他認為拋體本身具有某種動力,推動物體前進,直到耗盡才趨於停止,這種看法後來發展為14世紀的“衝力理論”。
14世紀,法國哲學家
布里丹(
Jean Buridan,1295—1358?)、阿爾伯特、尼克爾·奧里斯姆(
Nicole Oresme,1320?—1382)等人提出“衝力理論”,他們認為:“推動者在推動一物體運動時,便對它施加某種衝力或某種動力,速度越大,衝力越大,衝力耗盡時,物體停止下來。”這一理論為義大利物理學家
伽利略·伽利雷(
Galileo Galilei,1564—1642)和英國物理學家
艾薩克·牛頓(
Isaac Newton,1643—1727)開闢了道路。
17世紀,伽利略在其的著作中多次提出類似於
慣性原理的說法。他分別於1632年和1638年,在《
關於托勒密和哥白尼兩大世界體系的對話》和《
關於力學和位置運動的兩門新科學的對話》中記錄了理想斜面實驗(
一小球沿傾斜平台滾向水平面,表面越光滑小球滾得越遠),並推理“如有一足夠長而絕對光滑的表面,將沒有東西(
摩擦力)能阻礙小球運動,所以小球一直繼續運動或者直到有東西(
外力)阻礙它”,從而得到結論:“物體在自然狀態下會維持原有運動而非趨於停止”。該結論打破了自亞里士多德以來約一千三百年間“力是維持物體運動的原因”的陳舊觀念,但仍未擺脫其影響。該結論很接近慣性定律(
牛頓第一運動定律又稱慣性定律,其首先是由伽利略發現的)。
1644年,法國物理學家
勒內·笛卡爾(
Rene Descartes,1596—1650)在《
哲學原理》中彌補了伽利略的不足。他明確地指出,除非物體受到外因的作用,物體將永遠保持其靜止或運動狀態,並且還特地聲明,慣性運動的物體永遠不會使自己趨向曲線運動,而只保持在直線上運動。他把這條基本原理表述為兩條定律:①每一單獨的物質微粒將繼續保持同一狀態,直到與其他微粒相碰被迫改變這一狀態為止;②所有的運動,其本身都是沿直線的。然而笛卡兒沒有建立起他試圖建立的那種能演繹出各種自然現象的體系,不過他的思想對牛頓對此類定律之後的總結產生了一定的影響。笛卡兒的最大貢獻在於他第一個認識到:力是改變物體運動狀態的原因。
1662年,伽利略指出:“以任何速度運動著的物體,只要除去加速或減速的外因,此速度就可以保持不變。”笛卡爾也認為:“在沒有外加作用時,粒子或者勻速運動,或者靜止。”牛頓把這一假定作為
牛頓第一運動定律,並將伽利略的思想進一步推廣到有力作用的場合,提出了
牛頓第二運動定律。
1664年,牛頓受到對
碰撞問題研究較早的笛卡爾的影響,也開始研究二個球形非彈性
剛體的碰撞問題。1665
—1666年,牛頓又研究了二個球形剛體的碰撞問題。他沒有把注意力集中在
動量和
動量守恆方面,而是把集中在物體之間的相互作用上。對於兩剛體的碰撞,他提出:“在它們向彼此運動的時間中(就是它們相碰的瞬間),它們的壓力處於最大值,……它們的整個運動是被此一瞬間彼此之間的壓力所阻止,……只要這兩個物體都不互相屈服,它們之間將會持有同樣猛烈的壓力,……它們將會像以前彈回之前彼此趨近那樣多的運動相互離開。”
1668
—1669年,荷蘭物理學家
克里斯蒂安·惠更斯(
Christiaan Huygens,1629—1695)、沃里斯(
willis)和英國物理學家
克里斯托弗·雷恩(
Christopher Wren,1632—1723)分別對
碰撞問題也做了很多研究,並得出了一些重要的結論。其中,惠更斯的工作比較突出,他證明了兩硬體在碰撞過程中同一方向的動量保持不變,糾正了笛卡爾不考慮動量具有方向性的錯誤,而且首次提出碰撞前後的
動量守恆。牛頓在正式提出
牛頓第三運動定律時,肯定了他們的工作,同時也指出了他們的局限性。牛頓認為:“雷恩和惠更斯的理論以絕對硬的物體為前提,而用理想彈性體可以得到更肯定的結果,並且用非
理想彈性體,如壓緊的木球、鋼球和玻璃球做實驗,消除誤差後結果是一致的。”
1673年,法國物理學家
馬里奧特(
EdmeMarotte,1620—1684)用兩個
單擺做碰撞實驗,巧妙地測出了碰撞前後的瞬時速度。牛頓也重複做了此實驗,他進一步討論了
空氣阻力的影響及改進辦法,並對結果進行了修正。
1684年8月起,在英國物理學家
埃德蒙多·哈雷(
EdmondHalley,1656—1742)的勸說下,牛頓開始寫作《
自然哲學的數學原理》,系統地整理手稿,重新考慮部分問題。1685年11月,形成了兩卷專著。1687年7月5日,《原理》使用拉丁文出版。《原理》的緒論部分中的運動的公理或定律一節中提出了牛頓運動定律,擺脫了舊觀念的束縛。1713年,《原理》出第2版;1725年,出第3版。
19世紀後半期,德國物理學家
古斯塔夫·羅伯特·基爾霍夫(
Gustav Robert Kirchhoff,1824—1887)、奧地利及捷克物理學家
恩斯特·馬赫(
Ernst Mach,1838—1916)、美國物理學家埃森布德(
L. Eisenbud)、美國物理學家奧斯頓(
N. Austern)等人對牛頓運動定律的表述均有論述,並提出自己的修正意見。其中,馬赫在《發展中的力學》中,對牛頓運動定律做了比較全面的考察和分析整理;埃森布德在《關於經驗的運動定律》中、奧斯頓在《牛頓力學的表述》中,也提出了相似的新表述。但這些修正意見中有一部分受到質疑,質疑者包括瑞士及美國物理學家
阿爾伯特·愛因斯坦(
Albert Einstein,1879—1955)等。
套用領域
物體的受力情況已知求解運動狀態,或是運動狀態已知求解受力情況,均是對受力情況、加速度、運動狀態三個條件(結論)依次轉化,兩類問題的求解思路相同,基本分為以下三步:①確定研究對象,進行受力分析或運動狀態變化情況分析;②建立合適坐標系,列牛頓運動定律方程,適當補列其它方程;③解方程並討論。
除動力學領域外,牛頓運動定律在物理學其他分支學科上亦有套用。
在
流體力學中,牛頓運動定律較
功能原理,推導
理想流體的氣體沿水平方向運動或不計單位體積質量氣體的勢能時遵循的
伯努利方程 ,
85更直觀易懂。對於密度為
的小體元,設其受到的體積力密度為
,壓強梯度力為
,則牛頓第二運動定律在流體力學中有特殊表達形式:
。(式中
為梯度算符
。
也可能記作
,此時
表示
方向壓強的改變。)另外,基於通過對應力與應變線性定律進行修正而得到的唯象模型得到的
非牛頓流體的本構方程,可基於牛頓運動定律建立動能質氣擴散輸運的動量平衡方程得到,即適用於非牛頓流動的普適動量輸運定律,該方式還可闡明一些非牛頓流動現象的本質是來自能質運動過程中的慣性。
在
電磁感應中電容負載平行導軌模型中,接不同負載其上的導體棒將有不同的運動形式。接容抗時對電容器充電,其中導體棒只要有電流,則始終受
安培力,可以針對具體物理過程靈活運用牛頓運動定律及同一直線矢量合成方法確定桿的運動狀態。
在
機械製造領域中,牛頓運動定律能幫助研發安全且高效的機械結構或產品。根據牛頓第二運動定律推得的法向壓強梯度表達式
,能更好地解釋機翼舉力;根據牛頓第三運動定律導出的在運動時
,可設計出“空吸(卷吸)作用”原理設計的
尾噴管。上述兩種研究成果可廣泛用於指導飛機、火箭和車輛等運動機械的製造設計,對於提高它們的推進效率都會大有幫助。
在信息社會學領域中,借鑑牛頓運動定律的思想方法,可完成信息社會學有關概念的衍生與定理的變通,獲得的新規律可指導圖書情報工作的現狀與趨勢。
在
心理健康教育領域中,牛頓的三條運動定律可分別對應“立志”、“修身”和“崇尚仁愛”三個教育環節。在牛頓力學中,三定律既相互獨立,又有體系內的一致性、完整性和相容性;在教育學中,這三個環節相輔相成、和諧統一。這對引導高校理工科學生重塑、最佳化和調整心理品質、狀態,有著積極的啟示作用。
在
金融領域中,牛頓運動定律也可用來解釋和預測金融發展動向。如在
股票市場投資中,就有三條與牛頓運動定律一一對應的定律:①除有外因,股價維持原有變化趨勢;②股價增速依市場,成比例地正向變化;③每位買家都是賣主。該預測與數據比較基本準確。
在
動畫製作領域中,由於牛頓運動定律表明力的作用是造成一切運動的根本原因,而
動畫是讓畫面運動的影視藝術,故牛頓運動定律在動畫藝術中占有重要的位置,是動畫中必不可少的研究對象。如在銀幕上表現出物體的重量感,完全取決於其受力運動時動畫的間隔距離,而不在動畫稿本身的美觀和逼真程度。這需要合理藉助牛頓運動定律,能增強動畫真實感。
定律影響
牛頓運動定律批駁了延續兩千多年的
亞里士多德等人關於力的概念的錯誤觀點,為確立正確的力的概念奠定了基礎。該定律最早科學地給出了
慣性質量、
力等經典力學中的幾個基本概念的定性定義,為由牛頓運動定律建立起來的
質點力學體系原理奠定了概念基礎。
牛頓運動定律中的第一定律是其它原理的前提和基礎,奠定了經典力學的概念基礎,從而使它處於理論系統中第一個原理的前提地位。第二定律和
動量定理、
功能原理等,確定了物體運動狀態的變化與外界作用的關係。第三定律和
動量守恆定律等,將有關物體的運動關聯起來;和
萬有引力定律,開創了
天體力學,使人們第一次對日、月、星辰的運行規律有了準確的了解;給出了對
自然力的普遍陳述,揭示了兩物體相互作用的規律,為解決力學問題、轉換研究對象提供了理論基礎。

















 伽利略的理想斜面實驗
伽利略的理想斜面實驗 傾斜滑動法和水平拉線法
傾斜滑動法和水平拉線法 傾斜導軌法
傾斜導軌法 牛頓第二運動定律非線性擬合圖
牛頓第二運動定律非線性擬合圖 感測器定量實驗
感測器定量實驗 觀察法定性實驗
觀察法定性實驗