基本理論
洛倫茲變換是狹義相對論中兩個作
相對勻速運動的慣性參考系(
S和
S′)之間的
坐標變換。若
S系的坐標軸為
X、
Y和
Z,
S′系的坐標軸為
X′、
Y′和
Z′。為了簡單,讓
X、
Y和
Z軸分別平行於
X′、
Y′和
Z′軸,
S′系相對於
S系以不變速度
v沿
X軸的正方向運動,當
t=
t′ = 0 時,
S系和
S′系的原點互相重合。同一個
物理事件在
S系和
S′系中的時空坐標由下列關係式相聯繫:
這個關係式稱為洛倫茲變換。不同
慣性系中的
物理定律在洛倫茲變換下數學形式不變,它反映了
空間和
時間的密切聯繫,是狹義相對論中最基本的關係。
研究歷史
由
麥克斯韋方程組可以得到
電磁波的
波動方程,由波動方程解出
真空中的
光速是一個
常數。按照經典力學的
時空觀,這個結論應當只在某個特定的絕對靜止的慣性參考系中成立,這個
參考系就是
以太。其它參考系中測量到的光速是以太中光速與
觀察者所在參考系相對以太參考系的速度的
矢量疊加。然而1887年的
邁克耳孫-莫雷
實驗測量不到地球相對於以太參考系的
運動速度。1904年,洛倫茲提出了洛倫茲變換用於解釋邁克耳孫-莫雷實驗。根據他的構想,觀察者相對於以太以一定速度運動時,以太(即空間介質)
長度在
運動方向上發生收縮,抵消了不同方向上的光速差異,這樣就解釋了邁克耳孫-莫雷實驗的零結果。
1905年以前已經發現一些
電磁現象與
經典物理概念相牴觸,它們是:①邁克耳孫–莫雷實驗沒有觀測到地球相對於以太的運動。②運動物體的
電磁感應現象表現出相對性——是
磁體運動還是
導體運動其效果一樣。③
電子的
慣性質量隨電子運動速度的增加而變大。此外,
電磁規律(
麥克斯韋方程組)在
伽利略變換下不是不變的,即是說電磁
定律不滿足
牛頓力學中的伽利略
相對性原理。修改和發展
牛頓理論使之能夠圓滿解釋上述新現象成為19世紀末、20世紀初的當務之急。以H.洛倫茲為代表的許多
物理學家在
牛頓力學的框架內通過引入各種假設來對牛頓理論進行修補,最後引導出了許多新的與實驗結果相符合的方程式,如時間變慢和長度收縮
假說、質速關係式和
質能關係式,甚至得到了洛倫茲變換。所有這些公式中全都包含了真空光速。如果只為解釋已有的新現象,上述這些
公式已經足夠,但這些公式分別來自不同的假說或不同的
模型,而不是共同出自同一個
物理理論。而且,使用牛頓
絕對時空觀來對洛倫茲變換以及所含的真空光速進行解釋時卻遇到了概念上的困難。這種不協調的狀況預示著舊的物理觀念即將向新的物理觀念的轉變。在洛倫茲理論中,變換所引入的量僅僅是
數學上的輔助手段,並不包含
相對論的
時空觀。
愛因斯坦洞察到解決這種不協調狀況的關鍵是
同時性的
定義,而牛頓時空理論(或伽利略變換)中的時間沒有辦法在
現實世界中實現。為使用光信號對鐘,愛因斯坦假定了單向光速是個常數且與
光源的運動無關(
光速不變原理)。愛因斯坦以觀察到的事實為依據,把伽利略相對性原理直接推廣為狹義相對性原理,立足於這兩條基本原理,著眼於修正
運動、時間、空間等基本概念,重新導出洛倫茲變換,並賦予洛倫茲變換嶄新的物理內容。在
狹義相對論中,洛倫茲變換是最基本的關係式,狹義相對論的
運動學結論和時空性質,如同時性的相對性、長度收縮、時間延緩、速度變換公式、
相對論都卜勒效應等都可以從洛倫茲變換中直接得出。如果速度
v比光速
с小很多,而且被觀察的
物體的運動速度也比光速小很多,則洛倫茲變換就與伽利略變換近似一樣。對於日常的力學現象,使用伽利略變換就可以了。然而,對於運動物體的
電磁現象,雖然物體的運動速度比光速小很多,但由於電磁相互作用的
傳播速度是光速,所以仍必須使用洛倫茲變換。
數學形式
洛倫茲提出洛倫茲變換是基於以太存在的前提的,然而以太被證實是不存在的,根據光速不變原理,相對於任何慣性參考系,光速都具有相同的數值。愛因斯坦據此提出了狹義相對論。在狹義相對論中,空間和時間並不相互獨立,而是一個統一的
四維時空整體,不同慣性參考系之間的變換關係式與洛倫茲變換在數學表達式上是一致的,即:
其中x、y、z、t分別是慣性坐標系S下的坐標和時間,x'、y'、z'、t'分別是慣性坐標系S'下的坐標和時間。v是S'坐標系相對於S坐標系的運動速度,方向沿X軸。
由狹義相對性原理,只需在上述洛倫茲變換中把v變成-v,x'、y'、z'、t'分別與x、y、z、t互換,就得到洛倫茲變換的反變換式:
洛倫茲變換是高速運動的巨觀物體在不同慣性參考系之間進行坐標和時間變換的基本規律。當
相對速度v遠小於光速
c時,洛倫茲變換退化為
經典力學中的伽利略變換:
x'=x-ut y'=y z'=z t'=t
所以,狹義相對論與經典力學並不矛盾,狹義相對論將經典力學擴展到了巨觀物體在一切運動速度下的普遍情況,經典力學只是相對論在低速時(v遠小於c)的近似情況。一般在處理運動速度不太高的物體時(如
天體力學中計算
行星的運行軌道),不需考慮到
相對論效應,因為用相對論進行處理時計算往往變得非常繁瑣,而結果與經典情況相差不大。當處理高速運動的物體時,比如
高能加速器中的
電子,則必須要考慮相對論效應對結果帶來的修正。
初等數學推導
基本公理
推導過程
洛倫茲變換可以由狹義相對性原理和光速不變原理推導出來。下面根據這兩個基本原理,推導坐標的變換式。
 狹義相對論
狹義相對論構想有兩個
慣性坐標系S系、
S'系,
S'系的原點
O'相對
S系的原點
O以速率
v沿
X軸正方向運動。任意一
事件在
S系、
S'系中的時空坐標分別為(
x,
y,
z,
t)、(
x',
y',
z',
t')。
t、
t'分別是
S系和
S'系時刻。兩慣性坐標系重合時,分別開始計時.
若x= 0,則x'+vt' =0。這是變換須滿足的一個必要條件,故猜測任意一事件的坐標從S'繫到S系的變換為
x=γ(x'+vt') (1)
引入
相對性原理,即不同慣性系的物理方程的形式應相同。故上述事件坐標從
S繫到
S'系的變換為
x'=γ(x-vt) (2)
y與y'、z與z'的變換可以直接得出,即
y'=y (3)
z'=z (4)
把(2)代入(1),解t'得
t'=γt +(1-γ2) x/γv (5)
在上面推導的基礎上,引入光速不變原理,以尋求γ的取值。
由重合的原點O(O')發出一束沿X軸正方向的光,設光束的波前坐標為(X,Y,Z,T)、(X',Y',Z',T')。根據光速不變原理,有
X=cT (6)
X'=cT' (7)
相對論的光速不變原理得出:坐標值X等於光速c乘時刻T,坐標值X'等於光速c乘時刻T'。(1)(2)相乘得
xx'=γ2(xx'-x'vt+xvt'-v2tt') (8)
以波前這一事件作為對象,則(8)寫成
XX'=γ2(XX'-X'VT+XVT'-V2TT') (9)
(6)(7)代入(9),化簡得洛倫茲因子
γ= (1-(v/c)2)-1/2 (10)
(10)代入(5),化簡得
t'=γ(t-vx/c2) (11)
把(2)、(3)、(4)、(11)放在一起,即S繫到S'系的洛倫茲變換
x'=γ(x-vt),
y'=
y,
 H.A.洛倫茲
H.A.洛倫茲 z'=z,
t'=γ(t-vx/c2) (12)
根據
相對性原理,由(12)得
S'繫到
S系的洛倫茲變換
x=γ(x'+vt'),
y=y',
z=z',
t=γ(t'+vx'/c2) (13)
群論推導
相對性原理和光速不變的物理
原理是狹義相對論通常的出發點。實際上洛倫茲變換並不取決於
光的
物理性質——最重要的是粒子間的作用的定域性:一
粒子對另外一粒子的影響作用不能任意快地
傳遞,而作用傳遞的
極限速度必須是在所有參考系一樣的速度,此速度等於真空中
光速。
1.
閉合:兩個參考系轉換疊加得另外一轉換。以[
K→K']寫
K到
K'。對於任意三個參考系
[K→K''] = [K→K'][K'→K''] 。
2.
結合律:[
K→K'] ([
K'→K''][
K''→K''']) = ([K→K'] [K'→K''])[K''→K'''] 。4.
逆元:對任何參考系轉換 [
K→K'] 都有返回原本參考系的轉換[
K'→K] 。
參考系K'的原點O'在參照系K的運動:
得 Λ21 + vΛ22 = 0
同樣參照系K的原點O在參照系K'的運動:
得 Λ21+vΛ11= 0
因此主斜兩項相等且可稱為γ ≡Λ11= Λ22。還有 Λ21= -vγ :
當然逆轉換隻等同於反方向同速的轉換。運用上段γ的性質
每項比較得到:γ2+Λ12vγ= 1
從群的閉合性要求連續兩次轉換等於以速度和的單次轉換,也就是說兩個矩陣的積:
必須擁有同樣的
矩陣型式。這意味著
主斜線上兩項相等。因此以下比例:
γ= (1 +kv2)-1/2
這裡c2=∣k∣-1就是轉換的不變速度。如果k >0,c是一個速度的下限,明顯與物理現實不符,因此k≤0。但還可以分成k= 0和k < 0兩種情形:
k= 0得伽利略變換矩陣:
在更一般c = (-k)-1/2 小於無窮大的情況就得到洛倫茲變換矩陣:
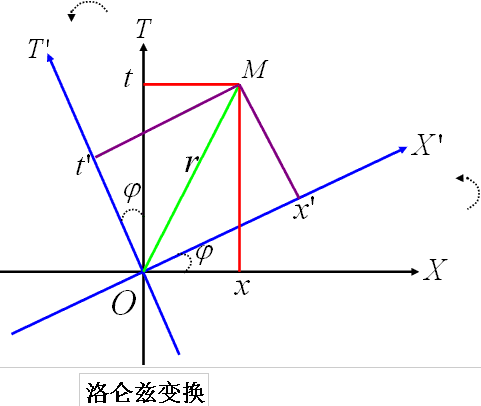
幾何理解
雖然矢量的坐標在不同坐標系裡面不一樣,它的
長度不變:(
x')
2+(
y')
2= (
x)
2+(
y)
2 。如果以另外角度
φ再旋轉一次,那矢量
新坐標和原坐標關係為:
可以相似般把洛倫茲變換看成一種類似的
坐標旋轉。定義
快度w= arctanh
β。那以上洛倫茲變換
公式可以寫成(略去不受影響的
x2和
x3):
也就是說,洛倫茲變換
數學上等同於雙曲角
旋轉。此坐標“旋轉”中類似“長度”的不變數是:
(x'0)2-(x'1)2= (x0)2-(x1)2 。
四維矢量形式
利用
w=
ict 將
事件坐標 (
t,
x,
y,
z) 改寫為
四維矢量 (
w,
x,
y,
z),則其模方是洛倫茲不變數(時空距離的
相反數),此時洛侖茲變換成為該矢量的
旋轉變換。用
方程組描述,就是




 狹義相對論
狹義相對論 H.A.洛倫茲
H.A.洛倫茲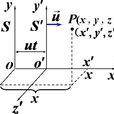





 狹義相對論
狹義相對論 H.A.洛倫茲
H.A.洛倫茲